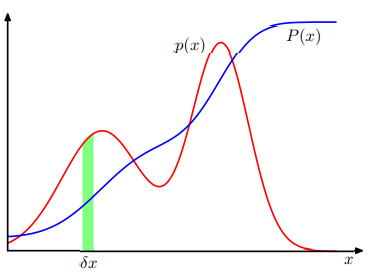
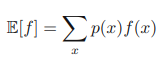오차 최소화 측면에서의 곡선 피팅 오차 최소화 측면에서의 곡선 피팅 곡선 피팅 N개의 관찰값 x로 이루어진 훈련 집합 x ≡ (x1,...,xN )T와 그에 해당하는 표적값 t ≡ (t1,...,tN )T가 주어졌다고 가정하자. 다음 그래프는 N=10 이고, sin(2πx) 함수에 가우시안 노이즈를 첨가 mldiary.tistory.com 확률적 측면에서의 곡선 피팅 확률적 측면에서의 곡선 피팅 앞선 글에서 다항식 곡선 피팅 문제를 오차 최소화의 측면에서 살펴보았다. 여기서는 같은 피팅 문제를 확률적 측면에서 살펴본다. 곡선 피팅 문제의 목표는 N개의 입력값 x = (x1, ... , xN)^T과 해 mldiary.tistory.com 앞서 소개한 다항식 곡선 피팅에서는 입력 변수가 오직 x 하나였다. ..