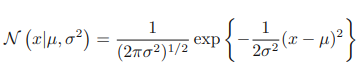
가우시안 분포는 단일 실수 변수 x에 대해 다음과 같이 정의된다(µ와 σ는 그래프의 개형을 결정짓는 변수이다).
µ는 평균 σ^2은 분산, σ는 표준 편차에 해당한다. 또한 분산의 역수에 해당하는 값 β는 정밀도라고 한다(β = 1/σ^2)
위의 식으로부터 가우시안 분포가 두 조건을 만족한다는 것을 알 수 있다.

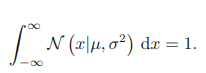
가우시안 분포를 따르는 x에 대한 함수의 기댓값은 다음과 같이 구할 수 있다.
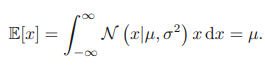
연속 변수로 이루어진 D차원 벡터 x에 대한 가우시안 분포는 다음과 같다.
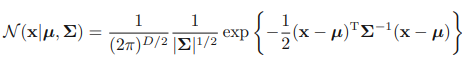
D차원 벡터 µ는 평균값, D x D행렬 Σ는공분산이라 한다. |Σ|는 행렬식이다.
관측된 데이터 집합을 바탕으로 확률 분포의 매개변수를 결정하는 방법 중 하나는 가능도 함수를 최대화하는 매개 변수(µ, σ^2)를 찾는 것이다. 관측된 데이터 집합에 대한 가능도 함수는 다음과 같다.
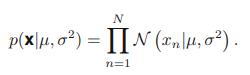
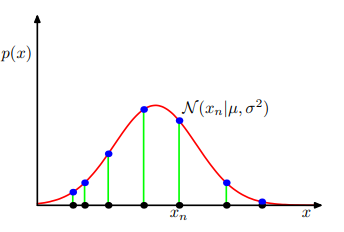
최대 가능도를 찾는 방법으로 µ, σ^2를 결정하는 것은 다음 그림을 통해 시각적으로 확인할 수 있다.
가능도 함수를 최대화시키는 방법으로 매개 변수를 찾는 과정을 계속해보자. 로그 함수는 변수에 대해 단조 증가하는 함수이므로 최대값/최소값을 찾을때 사용해도 된다. 따라서 최대 가능도 함수에 자연로그를 씌우면 다음과 같아진다.

위의 식에서 µ에 대해 미분한 값을 0으로 두면 최대 가능도 해 µML을 찾을 수 있다.
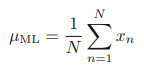
이를 바로 관찰된 값들의 평균인 표본 평균이라고 한다.
비슷한 방법으로 σ^2도 최대 가능도 해를 찾을 수 있다.
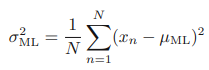
이를 표본 평균에 대해 계산된 표본 분산이라고 한다.
앞에서 최대 가능도를 이용하여 관측된 데이터집합의 가우시안 분포 매개변수 µ, σ^2를 찾아 보았다. 그러나 최대 가능도를 이용하여 가우시안 분포를 정의한느 것은 한계를 가지고 있다. 관측된 데이터 집합의 값에 대해 이들의 기댓값을 고려해보자.

계산 과정이 생략되어 왜 기댓값 앞에 (N-1)/N이 추가되었는지는 명확히 이해되지 않을 수 있으나 결과를 보면 최대 가능도 방법은 분산을 (N-1)/N만큼 과소평가하게 된다. 아래 그림을 통해 자세히 이해해보자.

녹색 그래프는 실제 데이터의 분포를 나타내고 파란 점은 관측된 데이터를 나타낸다. a, b, c 각각의 경우 두 개의 데이터 포인트가 관측되었다. 빨간색 정규 분포 그래프는 관측 데이터를 통해 예측한 정규 분포 그래프이다.
실제 데이터의 분포인 녹색 그래프는 분산이 매우 높은 그래프의 형태를 띄고 있다. 그러나 a, b, c 모두 분산이 낮은 뾰족한 그래프를 띄고 있다. a, b, c의 결과를 조합하여 평균을 내면 평균은 비슷하게 추정하고 있는 것을 알고 있으나 분산은 정확하게 추정하지 못하는 모습을 보인다. 왜냐하면 표본 분산은 실제 평균값이 아닌 표본 평균값을 기준으로 계산하기 때문이다. 여기서 분산을 과소평가하는 최대 가능도 방법의 단점이 드러난다.
물론, 위의 기댓값 식에서도 나타나 있지만 최대 가능도 방법은 분산을 (N-1)/N만큼 무시한다. 즉, N이 매우 커지면, 그 값 (N-1)/N의 값은 1에 수렴하므로 크게 문제되지 않는다는 것이다. 그럼에도 모델이 복잡해짐에 따라 다음과 같은 편향 문제는 더욱 심각해진다.
※이 글은 Christopher Bishop 교수님의 Pattern Recognition & Machine Learning을 공부하고 정리한 글입니다.
'Mathematics > probability' 카테고리의 다른 글
| 베이지안 확률 관점, 빈도적 확률 관점 (0) | 2023.01.26 |
|---|---|
| 기댓값과 공분산 (1) | 2023.01.26 |
| 확률 밀도 (0) | 2023.01.26 |
| 조건부 확률과 베이즈 정리 (0) | 2023.01.25 |
| 합의 법칙(sum rule), 곱의 법칙(product rule) (0) | 2023.01.25 |