많은 경우에 우리는 확률을 '반복 가능한 임의의 사건의 빈도수'라는 측면에서 바라본다. 이러한 해석을 빈도적 관점(frequentist)이라 일컫는다. 이에 맞서는 개념으로 이번장에서 다룰 베이지안(Bayesian)관점이 존재한다.
어떤 불확실한 사건에 대해 고려해 보자. 예를 들어, '공룡은 운석 충돌로 인해 멸종했다.'와 같은 사건을 생각해 보자. 이러한 사건들은 여러 번 반복할 수 없다. 따라서 앞서 살펴본 과일 상자 예시처럼 확률을 정의하는 것이 불가능하다. 그러나 우리는 이러한 사건들에 대해 견해 즉, 사전 지식을 가지고 있다. 예를 들어 '몇 억년 전 운석 충돌의 흔적이 발견 되었다.'와 같은 증거가 있다. 이러한 증거의 발견으로 인해 우리는 가지고 있던 사전 지식을 수정해 나갈 수 있다. 그리고 새로운 증거가 주어질 때마다 우리는 해당 사건에 대한 불확실성을 수정하고 최적의 선택을 내리고 싶을 것이다. 이것을 가능하게 하는 방법론이 바로 확률의 베이지안 해석이다.
베이지안 방법론은 어떠한 사건에 대한 사전 지식을 토대로, 새로운 증거가 추가되었을 때 사전 지식에 새로운 증거를 추가하여 사후 지식을 생성해 낸다. 이렇게 만들어낸 사후 지식은 다시 사전 지식이 되어 그 다음 증거가 추가되면 다시 사후 지식이 되는 순환을 반복한다. 이는 식으로 다음과 같이 확인할 수 있다.
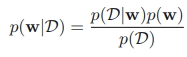
위의 식은 https://mldiary.tistory.com/39 에서 간단하게 소개했다. 여기서 p(w|D)는 사후 확률, p(D|w)는 가능도, p(w)는 사전 확률이 된다. 우리가 어떤 사건에 대해 가지고 있는 사전 확률(사전 지식)을 p(w)라고 할 때 새로운 증거 D가 발견되었다고 하자. 그럼 우리는 사전 확률을 바탕으로 해당 증거가 얼마나 타당한 증거인지 계산하고 이를 통해 사후 확률 p(w|D)를 계산해 낸다.
이러한 방식을 머신 러닝, 패턴 인식에 적용할 수 있다. 위의 베이즈 정리를 곡선 피팅 문제로 생각하여 다시 보자. w를 우리가 제어할 매개변수 즉, 기울기, D가 관측된 타겟값이라고 가정하자. 그러면, 해당 식은 D를 관측한 후의 w에 대한 불확실성을 사후 확률 p(w|D)로 표현한 것이 된다.
베이지안 정리의 오른쪽에 있는 값 p(D|w)는 관측 데이터 집합 D를 바탕으로 계산된다. 이 값은 매개변수 벡터 w의 함수로 볼 수 있으며, 가능도 함수(likelihood function)라고 불린다. 가능도 함수는 각각의 다른 매개변수 벡터 w에 대해 관측된 데이터 집합이 얼마나 '그렇게 나타날 가능성이 있었는지'를 표현한다. 가능도 함수는 w에 대한 확률 분포가 아니며, 따라서 w에 대해 가능도 함수를 적분하여도 1이 될 필요가 없다. 가능도 함수에 대한 정의를 바탕으로 베이지안 정리를 다음과 같이 적을 수 있다.
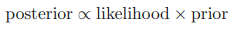
위의 식의 각 값은 모두 w에 대한 함수다. 앞서 소개한 베이즈 정리의 양쪽 변을 w에 대해 적분하면 베이지안 정리의 분모를 사전 확률과 가능도 함수로 표현할 수 있다.

위 식은 베이지안 정리의 분모와 사후 확률의 위치를 바꾼 후 적분하는 것으로 나타난 식이다. 사후 확률 p(w|D)는 w에 대한 확률이므로 w에 대해 적분하면 1이 되므로 위와 같이 유도가 가능하다.
가능도 함수 p(D|w)는 빈도적 관점과 베이지안 관점 양측에서 모두 중요한 역할을 차지한다. 하지만 가능도 함수가 사용되는 방법은 근본적으로 다르다.
빈도적 관점에서는 w가 고정된 매개변수로 여겨지며, 그 값은 추정값을 통해서 결정된다. 그리고 추정에서의 오류는 가능한 데이터 집합들 D의 분포를 고려함으로써 구할 수 있다.
베이지안 관점에서는 이와 대조적으로 오직 하나의 데이터 집합 D만이 존재하고 매개변수의 불확실성은 w의 확률 분포를 통해 표현된다.
빈도적 확률 관점
빈도적 확률 관점에서 널리 사용되는 추정값 중 하나는 바로 최대 가능도(maximum likelihood)이다. 최대 가능도 방법을 사용할 경우 w는 p(D|w)를 최대화 하는 값으로 선택된다. 음의 로그 가능도 함수를 오차 함수로 정의하기도 하는데 이는 빈도적 관점에서 가능도 함수를 최대화 시키는 것이 목표이므로 음의 가능도 함수를 최소화하는 것이 목표이므로 오차 함수를 최소화하는 것과 일치한다.
베이지안 확률 관점
베이지안 관점의 장점 중 하나는 사전 지식을 추론 과정에 포함시킬 수 있다는 것이다. 예를 들어 멀쩡한 동전 하나를 세 번 던졌는데, 세 번 다 앞면이 나왔다고 해보자. 최대 가능도 추정을 이용하면 당연히 앞면이 나올 확률이 1이라고 추정할 것이다. 하지만 베이지안 관점은 사전 지식을 포함하여 추정하기 때문에 그렇게 극단적인 값이 나타나지는 않을 것이다.
베이지안 관점의 대표적인 비판 중 하나는 사전 확률이 실제로 사전 지식을 나타내기 위해서가 아닌, 수학적 편리성을 위해 선택되는 경우가 많다는 것이다. 즉, 실제로 우리가 해당 확률에 대한 믿음을 전적으로 반영한 분포를 사용하는 것이 아니라, 계산이 편리하고 켤레성을 띄는 분포를 사용하기 때문에 사전 지식을 완전히 반영시키지 못한다는 것이다. 또한 만약 사전 지식을 온전히 반영한다고 하더라도 사전 지식 자체가 잘못되었을 수도 있다.
두 확률에 대한 관점 모두 어느것이 옳다고 할 수 없으며 특정 상황에 알맞는 접근 방법을 이용하는 것이 옳다.
'Mathematics > probability' 카테고리의 다른 글
| 가우시안 분포 (0) | 2023.01.27 |
|---|---|
| 기댓값과 공분산 (1) | 2023.01.26 |
| 확률 밀도 (0) | 2023.01.26 |
| 조건부 확률과 베이즈 정리 (0) | 2023.01.25 |
| 합의 법칙(sum rule), 곱의 법칙(product rule) (0) | 2023.01.25 |