합의 법칙
다음 그림과 같은 상황을 고려해보자

행 방향이 확률 변수 X가 가질 수 있는 값 xi이고 열 방향이 확률 변수 Y가 가질 수 있는 값 yj이다.
여기서, X=xi이면서 Y=yj일 확률을 p(X=xi, Y=yj)로 적고 결합 확률이라고 칭한다. 이 결합 확률은 다음과 같이 표현된다.

여기서 nij는 xi이면서 yi일 경우의 수를 뜻하고 N은 전체 가능한 경우의 수를 뜻한다.

위의 그림을 통해서 다음과 같은 식 또한 도출할 수 있다. 위의 두 식을 이용하여 다음을 도출할 수 있다.

이것이 확률의 합의 법칙이다. 때때로 p(X=xi)는 주변 확률이라고 불린다.
곱의 법칙
X=xi인 사례들만 고려해보자. 그 중 Y=yj인 사례들의 비율을 생각해 볼 수 있다. 이를 조건부 확률이라고 하며
p(Y=yj | X=xi)로 적을 수 있다. 이는 "X=xi일 때 Y=yj일 확률"로 해석된다. 이 조건부 확률도 위의 그림을 통해 다음과 같이 구할 수 있다.

위의 식들을 이용하여 다음을 도출해 낼 수 있다.
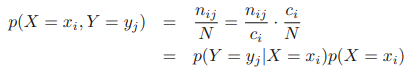
이것이 확률의 곱의 법칙이다.
표현을 간소화하여 다음과 같이 정리할 수 있다.

'Mathematics > probability' 카테고리의 다른 글
| 가우시안 분포 (0) | 2023.01.27 |
|---|---|
| 베이지안 확률 관점, 빈도적 확률 관점 (0) | 2023.01.26 |
| 기댓값과 공분산 (1) | 2023.01.26 |
| 확률 밀도 (0) | 2023.01.26 |
| 조건부 확률과 베이즈 정리 (0) | 2023.01.25 |