확률 밀도 p(x)하에서 어떤 함수 f(x)의 평균값은 f(x)의 기댓값이라 하며 E[f]라 적는다. 이산 분포의 경우 기댓값은 다음과 같이 주어진다.
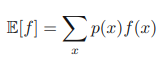
연속 변수의 경우에는 해당 확률 밀도에 대해 적분을 시행해서 기댓값을 구할 수 있다.
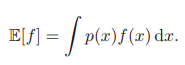
위의 기댓값에 대한 이해를 쉽게하기 위해 키를 예로 들어보자. 우리 나라 남성의 키를 확률 밀도 함수 p(x)로 나타내면, 170 중반을 중심으로 하는 정규 분포 형태의 그래프가 그려질 것이다. 만약 키의 평균 즉, 기대값을 구한다고 하면 위의 공식에서 f(x)는 단순히 x로 나타날 것이고 이를 계산하면 예측대로 E[f]는 170 중반의 값을 띄게 된다.
다변수 함수의 기댓값을 구할 경우에는 어떤 변수에 대해 평균을 내는지 지정하여 계산할 수 있다.
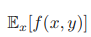
위의 식은 함수 f(x,y)의 평균값을 x의 분포에 대해 구하라는 의미이다. x의 분포에 대해 평균을 구하면 x는 사라지고 y만 남아 y에 관한 함수로 나타날 것이다.
또한 조건부 분포에 해당하는 조건부 기댓값도 생각해 볼 수 있다.
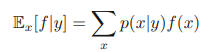
이는 연속 변수에 대해서도 마찬가지로 정의 내릴 수 있다.
f(x)의 분산은 다음과 같이 정의된다.
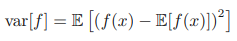
분산은 f(x)가 평균값 E[f(x)]로부터 얼마나 멀리 분포되어 있는지를 나타내는 값이다. 위 식을 전개하면 다음과 같이 분산을 f(x)와 f(x)^2의 기댓값으로 표현할 수도 있다.
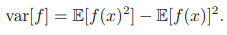
두 개의 확률 변수 x와 y에 대해서 공분산(covariance)은 다음과 같이 정의된다.
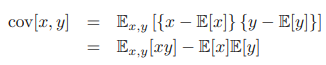
공분산은 x값과 y값이 얼마나 함께 같이 변동하는가에 대한 지표다. 만약 x와 y가 서로 독립적일 경우 공분산값은 0으로 간다.
두 확률 변수 x와 y가 벡터일 경우 공분산은 행렬이 된다.
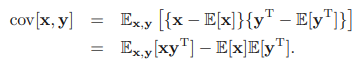
※이 글은 Christopher Bishop 교수님의 Pattern Recognition & Machine Learning을 공부하고 정리한 글입니다.
'Mathematics > probability' 카테고리의 다른 글
| 가우시안 분포 (0) | 2023.01.27 |
|---|---|
| 베이지안 확률 관점, 빈도적 확률 관점 (0) | 2023.01.26 |
| 확률 밀도 (0) | 2023.01.26 |
| 조건부 확률과 베이즈 정리 (0) | 2023.01.25 |
| 합의 법칙(sum rule), 곱의 법칙(product rule) (0) | 2023.01.25 |