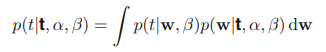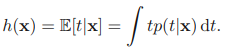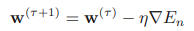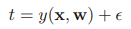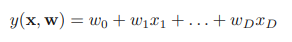ML Note

이전 글에서 직선 피팅 예시를 통해 베이지안 선형 회귀의 학습 방법을 알아 보았다. 베이지안 선형 회귀 - 직선 피팅 예시 (tistory.com) 베이지안 선형 회귀 - 직선 피팅 예시 선형 회귀 파라미터 최적화 - 최대 가능도 (tistory.com) 선형 회귀 파라미터 최적화 - 최대 가능도 선형 회귀의 파라미터 w를 최적화하기 위해 최대 가능도 방법을 이용해보자. 최대가능도를 이용한 mldiary.tistory.com 여기서는 w의 값을 알아내기 위해 학습을 반복했는데 실제 상황에서는 결국 새로운 x값에 대해 t의 값을 예측하는 것이 목표이다. 이를 위해서는 다음과 같이 정의되는 예측 분포(predictive distribution)를 고려해야 한다. t는 훈련 데이터로으로 이루어진 벡터이다. 이..

선형 회귀 파라미터 최적화 - 최대 가능도 (tistory.com) 선형 회귀 파라미터 최적화 - 최대 가능도 선형 회귀의 파라미터 w를 최적화하기 위해 최대 가능도 방법을 이용해보자. 최대가능도를 이용한 w 최적화 타깃 변수 t는 결정 함수 y(x,w)와 가우시안 노이즈의 합으로 주어진다고 가정하자. 여 mldiary.tistory.com 위의 글에서 빈도적 접근으로 선형 회귀 문제를 풀어보았다. 그러나 빈도적 접근에는 항상 따라붙는 문제가 있는데 바로 과적합(over fitting) 문제이다. 이를 극복하기 위해 정규화항을 추가하여 모델 복잡도를 조정하는 방법이 있었으나 이 마저도 문제인게, 이제는 과적합을 해결하기 위해 모델 복잡도를 잘 조정해야하는 문제가 생긴다. 따라서 빈도적 관점에서의 접근은 ..

이번 글에서는 편향 분산 트레이드 오프(bias various trade off)에 대해 알아본다. 과적합 문제는 최대 가능도 방법을 사용할 경우에 동반될 수밖에 없는 성질이다. 최대 가능도와 같은 빈도주의 관점 모델은 이러한 문제를 항상 고려해야 하는데, 이러한 모델의 복잡도에 대해 편향 분산 트레이드 오프라 일컫는다. 회귀 문제에서 최적의 예측치 h(x)를 구한다고 하자. h(x)는 다음과 같이 나타난다. 이를 이용하여 기대 제곱 오류를 다음 형태로 적을 수 있음을 이전 글에서 증명했다. 여기서 두 번째 항은 y(x)와 독립적으로, 데이터의 내재적 노이즈로부터 생겨난 것이며, 기대 오륫값이 도달할 수 있는 가장 최소의 값에 해당한다. 첫 번째 항의 값은 함수 y(x)로 어떤 것을 선택하느냐에 따라 결..

오차 최소화 측면에서의 곡선 피팅 :: ML Note (tistory.com) 오차 최소화 측면에서의 곡선 피팅 곡선 피팅 N개의 관찰값 x로 이루어진 훈련 집합 x ≡ (x1,...,xN )T와 그에 해당하는 표적값 t ≡ (t1,...,tN )T가 주어졌다고 가정하자. 다음 그래프는 N=10 이고, sin(2πx) 함수에 가우시안 노이즈를 첨가 mldiary.tistory.com 위의 글에서 과적합을 막기 위해 오류 함수에 정규화항을 추가하는 아이디어에 대해 소개했었다. 이를 포함한 오류 함수는 다음 형태를 띄게 된다. 여기서 λ는 데이터에 종속적인 에러 ED(w)와 정규화항 EW(w)의 상대적 중요도를 조절하기 위한 정규화 상수다. 가장 단순한 형태의 정규화항은 가중치 벡터 원소들의 제곱합이다. 이..

최대가능도 선형 회귀 파라미터 최적화 - 최대 가능도 선형 회귀의 파라미터 w를 최적화하기 위해 최대 가능도 방법을 이용해보자. 최대가능도를 이용한 w 최적화 타깃 변수 t는 결정 함수 y(x,w)와 가우시안 노이즈의 합으로 주어진다고 가정하자. 여 mldiary.tistory.com 위의 글에서 살펴본 것처럼 최대 가능도 해와 같이 일괄 처리 테크닉을 활용하기 위해서는 전체 데이터셋을 한 번에 처리해야 한다. 하지만 큰 데이터셋에 있어 이러한 방식이 계산적으로 어려울 수 있다. 이런 경우 순차적 알고리즘을 활용하는 것이 나을 수 있다. 이러한 방식을 확률적 경사 하강법(Stochastic Gradient Descent)이라고 부른다. 이 방법으로 w를 다음과 같이 업데이트 할 수 있다. 여기서 τ는 반..

선형 회귀의 파라미터 w를 최적화하기 위해 최대 가능도 방법을 이용해보자. 최대가능도를 이용한 w 최적화 타깃 변수 t는 결정 함수 y(x,w)와 가우시안 노이즈의 합으로 주어진다고 가정하자. 여기서 e는 0을 평균으로, β(분산의 역)을 정밀도로 가지는 가우시안 확률 변수이다. 따라서 다음과 같이 적을 수 있다. 위의 식은 t에 대한 확률 분포로, 우변을 보면 y(x,w)결정 함수와, 정밀도에 의해 정의 되는 가우시안 분포로 나타나는 것을 확인할 수 있다. 이제 여러 개의 입력 데이터셋을 가정해보자. X = {x1, ... , xN}이고 t ={t1, ... , tN}이라고 가정한다. 이 때 가능도 함수를 다음과 같이 구할 수 있다. t의 가능도 함수는 입력 데이터셋의 가우시안 분포를 전부 곱한 것으로..

가장 단순한 형태의 선형 회귀 모델은 입력 변수들의 선형 결합을 바탕으로 한 모델이다. 이를 선형 회귀(linear regression) 모델이라고 부른다. 선형 회귀의 가장 중요한 성질은 매개변수 w0, ... , wD의 선형 함수라는 것이다. 또한 이 모델은 입력 변수 xi의 선형 함수이기도 한데, 바로 이 성질 때문에 선형 회귀 모델에는 심각한 한계점이 존재한다. 이러한 한계점을 극복하기 위해 다음처럼 입력 변수에 대한 고정 비선형 함수들의 선형 결합을 사용할 수 있다. 여기서 φj (x)가 기저 함수(basis function)이다. 이 모델의 배개변수의 총 숫자는 M-1 + 1(w0) = M이 된다. 매개변수 w0은 데이터에 있는 편향을 표현할 수 있게 해준다. 따라서 편향 매개변수라고 부르기도..

분류 문제 결정 이론 세 가지 결정 이론(오분류 비율 최소화, 기대 손실 최소화, 거부 옵션) 결정 이론(decision theory)란 불확실성이 존재하는 상황에서 최적의 의사결정을 내리는 방법에 대한 이론이다. 특히 분류 문제에서 여러가지 label값들 중 하나의 값의 확률이 100%로 나타나는 것이 mldiary.tistory.com 위의 글에서 분류 문제를 기준으로 결정 이론을 살펴보았다. 회귀 문제에서도 결정 이론이 존재한다. 회귀 문제의 결정 단계에서는 각각의 x에 대해 t의 추정값 y(x)를 선택해야 한다. 이 과정에서 손실L(t,y(x))가 발생한다고 가정하자. 그러면 평균 기대 손실은 다음과 같이 주어진다. 분류 문제에서는 손실 값이 손실 행렬으로써 이산적으로 표현되었으나 회귀 문제에서는..

앞선 글에서 다항식 곡선 피팅 문제를 오차 최소화의 측면에서 살펴보았다. 여기서는 같은 피팅 문제를 확률적 측면에서 살펴본다. 곡선 피팅 문제의 목표는 N개의 입력값 x = (x1, ... , xN)^T과 해당 표적값 t = (t1, ... , tN)^T가 주어진 상황에서 새로운 입력 변수 x가 주어졌을 때 그에 대한 타깃 변수 t를 예측해 내는 것이다. 여기서 확률 분포를 이용하여(여기서는 가우시안 분포를 이용한다)타깃 변수의 값에 대한 불확실성을 표현할 수 있다. 이는 주어진 x값에 대해 피팅한 곡선 y(x,w)를 평균으로 가지는 정규분포를 이용하여 불확실성을 표현한다. 아래 그림으로 위의 설명을 직관적으로 이해할 수 있다. 위의 그림을 보면 x0지점에서 우리가 피팅한 빨간색 곡선을 중심으로 하는 정..

곡선 피팅 N개의 관찰값 x로 이루어진 훈련 집합 x ≡ (x1,...,xN )T와 그에 해당하는 표적값 t ≡ (t1,...,tN )T가 주어졌다고 가정하자. 다음 그래프는 N=10 이고, sin(2πx) 함수에 가우시안 노이즈를 첨가하여 만든 타겟값들이다. 우리의 목표는 훈련 집합 x를 이용하여 새로운 입력값 x가 들어왔을 때 타겟 변수 t를 예측하는 것이다. 해당 곡선을 피팅하는 데 있어 다음과 같은 형태의 다항식을 활용한다. 다항함수 y(x,w)는 x에 대해서는 비선형이지만, 계수 w에 대해서는 선형이다. 우리는 위의 그래프에 파란 점에 해당하는 학습 데이터를 이용하여 새로운 x값이 들어왔을 때 t를 예측할 것이다. 따라서 위의 다항식을 이용하여 데이터가 어떤 형태로 분포하는지 표현하는 것이 목표..