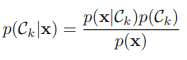ML Note

가장 단순한 형태의 선형 회귀 모델은 입력 변수들의 선형 결합을 바탕으로 한 모델이다. 이를 선형 회귀(linear regression) 모델이라고 부른다. 선형 회귀의 가장 중요한 성질은 매개변수 w0, ... , wD의 선형 함수라는 것이다. 또한 이 모델은 입력 변수 xi의 선형 함수이기도 한데, 바로 이 성질 때문에 선형 회귀 모델에는 심각한 한계점이 존재한다. 이러한 한계점을 극복하기 위해 다음처럼 입력 변수에 대한 고정 비선형 함수들의 선형 결합을 사용할 수 있다. 여기서 φj (x)가 기저 함수(basis function)이다. 이 모델의 배개변수의 총 숫자는 M-1 + 1(w0) = M이 된다. 매개변수 w0은 데이터에 있는 편향을 표현할 수 있게 해준다. 따라서 편향 매개변수라고 부르기도..

베타 분포 베타 분포 베르누이 분포, 이항 분포 이산 확률 변수 - 베르누이 분포, 이항 분포 베르누이 분포 동전 던지기 이진 확률 변수 x ∈ {0,1}을 고려해 보자. x=0은 뒷면, x=1은 앞면이다. 동전이 망가져서 앞면, 뒷 mldiary.tistory.com 이항 분포에서 사전 분포를 도입하기 위해 켤레성을 가지게 하는 베타 분포에 대해 알아보았다. 여기서는 이항 분포가 아닌 다항 분포에서 사전 분포를 도입하기 위해 켤레성을 가지게 하는 디리클레 분포에 대해 알아보자. (사전 분포를 도입하는 이유는 위의 글에서 설명했듯이 베이지안 접근법을 이용하여 불확실성을 표현하고자 하기 때문이다.) 다항 분포의 매개변수 {µk}에 대해 살펴보자. 다항 분포의 형태를 살펴보면 켤레성을 띄기 위해 사전 분포가..

지금까지는 두 가지 가능한 값들 중 하나를 취하는 수량을 설명하였다. 그러나 많은 경우 이진 변수가 아닌 서로 다른 K개의 값들 중 하나를 취할 수 있다. 여기서 이런 변수를 표현하는 대표적인 방법인 원-핫 인코딩을 알아보고, 이를 이용하여 다항 분포에 대해 설명한다. 원-핫 인코딩은 다음과 같이 벡터로 표현된다. 위의 예시는 총 6개의 값들 중 하나를 취할 수 있는 변수 x에 대해 나타낸 것이다. 이러한 벡터들은다음과 같은 성질을 만족한다. 만약 우리가 xk = 1이 될 확률을 µk라고 한다면, x의 분포는 다음과 같이 주어진다. 여기서 µ = (µ1, ... , µk)T이다. µk는 k번째 값을 가질 확률을 나타내게 된다. 이 분포에 대해 다음 두 가지 식을 쉽게 증명할 수 있다. 여기서 N개의 독립..

베르누이 분포, 이항 분포 이산 확률 변수 - 베르누이 분포, 이항 분포 베르누이 분포 동전 던지기 이진 확률 변수 x ∈ {0,1}을 고려해 보자. x=0은 뒷면, x=1은 앞면이다. 동전이 망가져서 앞면, 뒷면이 나올 확률이 동일하지 않다고 가정하자. 이때 x=1일 확률은 매개변 mldiary.tistory.com 위의 글에서 관측된 데이터를 토대로 최대 가능도 방법을 이용해 베르누이 분포와 이항 분포의 µ의 값을 추정하는 방법을 알아보았다. 그러나 여기서 구한 방법처럼 최대 가능도 방법(빈도적 관점)을 이용할 경우 관측 데이터에 심한 과적합을 일으킬 수 있다. 따라서 사전 분포를 도입하여(베이지안 관점) µ의 분포 p(µ)를 구하는 방법을 알아보자. 최대 가능도 방법은 µ에 대해 점추정을 하는 반면..

베르누이 분포 동전 던지기 이진 확률 변수 x ∈ {0,1}을 고려해 보자. x=0은 뒷면, x=1은 앞면이다. 동전이 망가져서 앞면, 뒷면이 나올 확률이 동일하지 않다고 가정하자. 이때 x=1일 확률은 매개변수 µ를 통해 다음과 같이 표현 가능하다. 여기에 다음 조건이 추가된다. 0

정보이론 정보 이론 정보 이론은 확률론 결정 이론 등과 함께 머신러닝 & 패턴인식에서 중요한 개념이다. 이번 글에서는 정보이론에 대해 소개한다. 이산확률 변수 x를 고려해보자. 이 변수가 특정 값을 가지고 있는 mldiary.tistory.com 위의 글에서 확률에서의 엔트로피의 개념에 대해 알아보았다. 이제 이 개념을 어떻게 패턴 인식에 활용할 수 있을 지 알아보자. 쿨백 라이블러 발산 알려지지 않은 분포 p(x)를 고려해보자. 이를 피팅하기 위해 모델을 만들었으며, (x)그 결과로 분포 q(x)를 구할 수 있었다고 하자. 만약 q(x)를 이용하여 x의 값을 수신자에게 전달하기 위해 코드를 만든다고 하면 p(x)가 아닌 q(x)를 사용했으므로 추가 정보가 필요하다. 이때 추가로 필요한 정보의 양은 다음..

정보 이론은 확률론 결정 이론 등과 함께 머신러닝 & 패턴인식에서 중요한 개념이다. 이번 글에서는 정보이론에 대해 소개한다. 이산확률 변수 x를 고려해보자. 이 변수가 특정 값을 가지고 있는 것을 확인했을 때 전달되는 정보의 양은 얼마만큼일까? 여기서 정보의 양은 '놀라움의 정도'로 생각할 수 있을 것이다. 매우 일어날 가능성이 높은 사건이 일어났다는 사실을 전해들었을 때보다 일어나기 매우 힘든 사건이 발생했다는 사실을 전해 들었을 때 더 많은 정보를 전달받는게 된다. 따라서 우리가 사용하게 될 정보량의 측정 단위는 해당 사건이 일어날 확률 p(x)의 종속적이게 된다. p(x)에 단조 함수인 정보량을 표현하는 함수 h(x)에 대해 살펴보도록 하자. 서로 연관되어 있지 않은(독립적인) 두 사건 x, y가 ..

분류 문제 결정 이론 세 가지 결정 이론(오분류 비율 최소화, 기대 손실 최소화, 거부 옵션) 결정 이론(decision theory)란 불확실성이 존재하는 상황에서 최적의 의사결정을 내리는 방법에 대한 이론이다. 특히 분류 문제에서 여러가지 label값들 중 하나의 값의 확률이 100%로 나타나는 것이 mldiary.tistory.com 위의 글에서 분류 문제를 기준으로 결정 이론을 살펴보았다. 회귀 문제에서도 결정 이론이 존재한다. 회귀 문제의 결정 단계에서는 각각의 x에 대해 t의 추정값 y(x)를 선택해야 한다. 이 과정에서 손실L(t,y(x))가 발생한다고 가정하자. 그러면 평균 기대 손실은 다음과 같이 주어진다. 분류 문제에서는 손실 값이 손실 행렬으로써 이산적으로 표현되었으나 회귀 문제에서는..

세 가지 결정 이론 세 가지 결정 이론(오분류 비율 최소화, 기대 손실 최소화, 거부 옵션) 결정 이론(decision theory)란 불확실성이 존재하는 상황에서 최적의 의사결정을 내리는 방법에 대한 이론이다. 특히 분류 문제에서 여러가지 label값들 중 하나의 값의 확률이 100%로 나타나는 것이 mldiary.tistory.com 지금까지 분류 문제를 두 개의 단계로 나누어 보았다. 첫 번째는 추론 단계(inference stage)로 훈련 데이터셋을 활용하여 p(Ck|x)에 대한 모델을 학습시키는 단계이다. 두 번째는 결정 단계(decision stage)로 학습된 사후 확률들을 이용해서 최적의 클래스 할당을 시행하는 것이다. 두 가지 문제를 한 번에 풀어내는 방법을 생각해 볼 수도 있는데, x..

결정 이론(decision theory)란 불확실성이 존재하는 상황에서 최적의 의사결정을 내리는 방법에 대한 이론이다. 특히 분류 문제에서 여러가지 label값들 중 하나의 값의 확률이 100%로 나타나는 것이 아니라면 예측 결과가 틀릴 수도 있는 위험에 처하게 된다. 이러한 불확실성이 존재하는 상황에서 결정을 내리는 3가지 방법론에 대해 소개한다. 결정 이론을 이해하고 비교하기 위해 다음과 같은 예시를 생각해보자. 환자의 엑스레이 이미지를 바탕으로 그 환자가 암에 걸렸는지 아닌지 판단하는 진단 문제를 고려해보자. 이 경우 입력 벡터 x는 이미지의 픽셀 강도 집합에 해당할 것이며, t는 환자가 암에 걸렸는지 아닌지를 나타내는 출력 변수일 것이다. 여기서는 환자에게 암이 있다고 판단할 경우에는 클래스 C1..