이산 확률 변수 - 베르누이 분포, 이항 분포
베르누이 분포 동전 던지기 이진 확률 변수 x ∈ {0,1}을 고려해 보자. x=0은 뒷면, x=1은 앞면이다. 동전이 망가져서 앞면, 뒷면이 나올 확률이 동일하지 않다고 가정하자. 이때 x=1일 확률은 매개변
mldiary.tistory.com
위의 글에서 관측된 데이터를 토대로 최대 가능도 방법을 이용해 베르누이 분포와 이항 분포의 µ의 값을 추정하는 방법을 알아보았다. 그러나 여기서 구한 방법처럼 최대 가능도 방법(빈도적 관점)을 이용할 경우 관측 데이터에 심한 과적합을 일으킬 수 있다. 따라서 사전 분포를 도입하여(베이지안 관점) µ의 분포 p(µ)를 구하는 방법을 알아보자. 최대 가능도 방법은 µ에 대해 점추정을 하는 반면 사전 분포를 이용한 베이지안 접근법에서는 µ의 불확실성을 포함하여 p(µ) 즉, µ의 분포로 나타나게 된다.
여기서 중요한 개념인 켤레성(conjugacy)에 대해 알아보고 넘어가자. 앞서 가능도 함수가 다음과 같이 나타나는 것을 확인하였다.
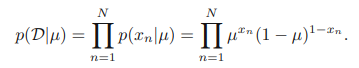
그리고 우리가 적용하고자 하는 베이지안 접근법은 다음과 같았음을 기억할 것이다.
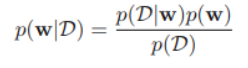
가능도 함수가 띄는 형태를 유심히 보자. 만약 사전 분포 p(µ)가 가능도 함수를 고려하여 µ와 (1-µ)의 거듭제곱에 비례하는 형태를 사전 분포로 선택한다면, 사전 확률과 가능도 함수의 곱에 비례하는 사후 분포 역시 사전 분포와 같은 함수적 형태를 띄게 될 것이다. 이러한 성질을 켤레성이라고 한다. 이렇게 사전 분포와 사후 분포가 켤레성을 띄면 사후 분포가 다시 사전 분포가 될 수 있다는 유용한 성질을 가지게 된다. 예를 들어 사전 분포 p(µ)가 있을 때, 관측 데이터를 적용하여 가능도 p(D|µ)를 구하였다고 하자. 이를 통해 우리는 사후 분포 p(µ|D)를 구할 수 있을 것이다. 그런데 만약 여기서 추가적인 데이터 D'를 발견하였다고 하자 그 경우, 우리는 사후 분포를 추가적으로 업데이트 할 수 있을 것이다. 이 경우 p(µ|D)를 사전 분포 p(µ)로 두고, 가능도 함수 p(D'|µ)로 설정한 후 베이즈 정리를 다시 한 번 이용하여 사후 분포 p(µ|D')를 구할 수 있을 것이다. 이렇게 추가적인 데이터가 발견됨에 따라 우리의 사후 믿음을 업데이트 해나갈 수 있어, 베이지안 정리를 용이하게 이용할 수 있다.
켤레성을 가지도록 사전 분포를 설정하는 것이 왜 중요한지 살펴보았다. 베르누이 분포의 가능도 함수를 고려하여 켤레성을 가지도록 사전 분포를 모델링한 것이 아래 나와있는 베타 분포이다.
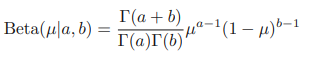
여기서 감마 함수는 다음과 같이 정의된다.
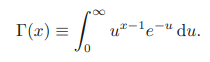
베타 분포의 계수들 (a, b)는 베타 분포가 졍규화되도록 한다.
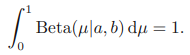
베타 분포의 평균과 분산은 다음과 같이 주어진다.
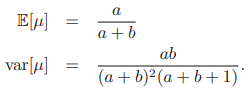
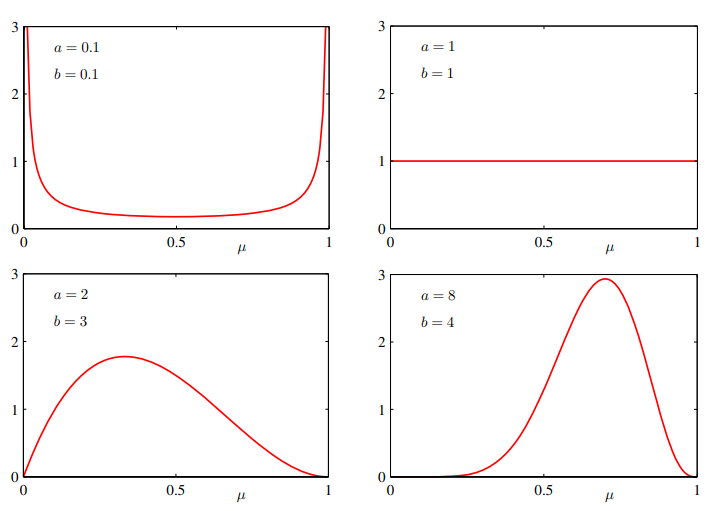
매개변수 a, b는 매개변수 µ의 분포를 조절하기 때문에 초매개변수(hyperparameter)이다. a, b 값에 따른 µ의 분포는 아래의 그림에서 확인할 수 있다.
이제, 베타 사전분포와 가능도함수를 곱하여 µ에 대한 사후 분포를 구할 수 있다. 이는 다음과 같은 형태로 정리된다.
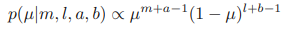
여기서 l = N-m이며 동전 던지기 예시에서 '뒷면'의 개수에 해당한다. 사후 분포가 사전 분포에 대해 같은 함수적 종속성을 가지는 것을 알 수 있다. 이를 켤레성을 가진다고 정의한다. 실제로 사후 분포는 단순히 또 다른 베타 분포일 뿐이다. 이 새로운 베타 분포의 정규화 계수는 다음과 같아진다.
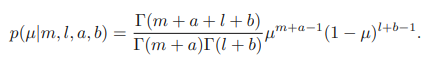
사후 분포에서 초매개변수 a는 m만큼 b는 l만큼 증가한 것을 알 수 있다. 이 사실로부터 사전 분포의 초매개변수 a, b를 각각 x=1, x=0인 경우에 대한 유효 관찰수로 해석할 수 있다. 여기서 만약 새로운 데이터가 추가된다면 지금의 사후 분포가 새로운 사전 분포가 될 수 있다. 이를 업데이트하는 방식이 아래 그림에 나타나있다.
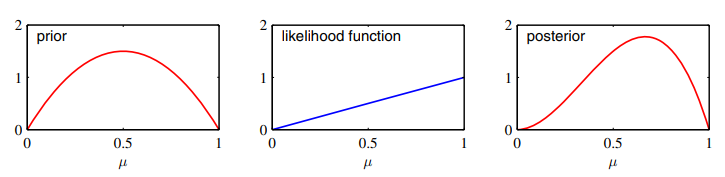
왼쪽이 사전 분포, 가운데가 가능도 함수, 오른쪽이 사후 분포이다. 처음 사전 분포는 0.5가 평균인 베타 분포이다. 가능도 함수를 통해서, 발견된 사건이 우리의 사전분포로부터 '얼마나 가능했는지'를 정의한다. 이를 사전 분포에 곱해 사후 분포를 계산한 결과 개형이 오른쪽으로 조금 더 치우쳐진 분포가 되었다.
베이지안 관점을 이용하면 학습에 있어 순차적(sequential)인 접근이 자연스럽게 여겨지게 된다.
만약 우리의 목표가 다음 시도의 결과값을 예측하는 것이라면 다음과 같이 할 수 있다.
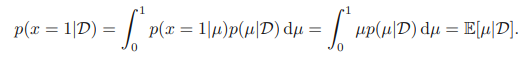
확률의 곱의 법칙을 이용하여 주변화시키고, 구해놓은 사후 분포를 이용하여 µ에 대한 기댓값을 구하였다. 이는 간단히 다음과 같이 정의된다.
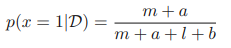
그런데 위의 a, b에 관한 네 가지 그래프를 살펴보면 a, b가 커질수록 즉, 관측 값의 개수가 많아질수록 그래프는 뾰족해지는 경향을 보이는 것 같다. 실제로도 그러할까? 이를 확인하기 위해 θ를 추정하는 베이지안 문제를 고려해보자. 이 문제는 결합 분포 p(θ,D)로 표현 가능하다. 기댓값은 다음과 같다.
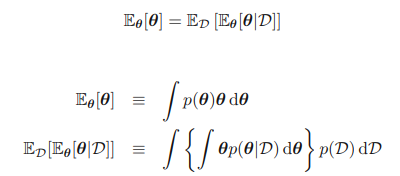
이로부터 데이터가 생성된 원 분포에 대해 평균을 낸 θ의 사후 평균값은 θ의 사전 평균과 같은 것을 알 수 있다.
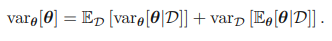
이제 분산을 살펴보자. 오른쪽 변의 첫 항은 θ의 사후 분산의 평균이며, 두 번째 항은 θ의 사후 평균의 분산에 해당한다. 따라서 이 결과에 따르면 평균적으로 θ의 사후 분산은 사전 분산보다 작다는 것을 알 수 있다.
'Mathematics > Statistics' 카테고리의 다른 글
| 디리클레 분포 (0) | 2023.01.30 |
|---|---|
| 다항 분포 (0) | 2023.01.30 |
| 이산 확률 변수 - 베르누이 분포, 이항 분포 (0) | 2023.01.29 |
| 상대 엔트로피, 쿨백 라이블러 발산(Kullback-Leibler divergence) (0) | 2023.01.29 |
| 정보 이론 (0) | 2023.01.28 |