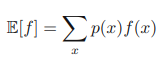ML Note

베타 분포 베타 분포 베르누이 분포, 이항 분포 이산 확률 변수 - 베르누이 분포, 이항 분포 베르누이 분포 동전 던지기 이진 확률 변수 x ∈ {0,1}을 고려해 보자. x=0은 뒷면, x=1은 앞면이다. 동전이 망가져서 앞면, 뒷 mldiary.tistory.com 이항 분포에서 사전 분포를 도입하기 위해 켤레성을 가지게 하는 베타 분포에 대해 알아보았다. 여기서는 이항 분포가 아닌 다항 분포에서 사전 분포를 도입하기 위해 켤레성을 가지게 하는 디리클레 분포에 대해 알아보자. (사전 분포를 도입하는 이유는 위의 글에서 설명했듯이 베이지안 접근법을 이용하여 불확실성을 표현하고자 하기 때문이다.) 다항 분포의 매개변수 {µk}에 대해 살펴보자. 다항 분포의 형태를 살펴보면 켤레성을 띄기 위해 사전 분포가..

지금까지는 두 가지 가능한 값들 중 하나를 취하는 수량을 설명하였다. 그러나 많은 경우 이진 변수가 아닌 서로 다른 K개의 값들 중 하나를 취할 수 있다. 여기서 이런 변수를 표현하는 대표적인 방법인 원-핫 인코딩을 알아보고, 이를 이용하여 다항 분포에 대해 설명한다. 원-핫 인코딩은 다음과 같이 벡터로 표현된다. 위의 예시는 총 6개의 값들 중 하나를 취할 수 있는 변수 x에 대해 나타낸 것이다. 이러한 벡터들은다음과 같은 성질을 만족한다. 만약 우리가 xk = 1이 될 확률을 µk라고 한다면, x의 분포는 다음과 같이 주어진다. 여기서 µ = (µ1, ... , µk)T이다. µk는 k번째 값을 가질 확률을 나타내게 된다. 이 분포에 대해 다음 두 가지 식을 쉽게 증명할 수 있다. 여기서 N개의 독립..

베르누이 분포, 이항 분포 이산 확률 변수 - 베르누이 분포, 이항 분포 베르누이 분포 동전 던지기 이진 확률 변수 x ∈ {0,1}을 고려해 보자. x=0은 뒷면, x=1은 앞면이다. 동전이 망가져서 앞면, 뒷면이 나올 확률이 동일하지 않다고 가정하자. 이때 x=1일 확률은 매개변 mldiary.tistory.com 위의 글에서 관측된 데이터를 토대로 최대 가능도 방법을 이용해 베르누이 분포와 이항 분포의 µ의 값을 추정하는 방법을 알아보았다. 그러나 여기서 구한 방법처럼 최대 가능도 방법(빈도적 관점)을 이용할 경우 관측 데이터에 심한 과적합을 일으킬 수 있다. 따라서 사전 분포를 도입하여(베이지안 관점) µ의 분포 p(µ)를 구하는 방법을 알아보자. 최대 가능도 방법은 µ에 대해 점추정을 하는 반면..

베르누이 분포 동전 던지기 이진 확률 변수 x ∈ {0,1}을 고려해 보자. x=0은 뒷면, x=1은 앞면이다. 동전이 망가져서 앞면, 뒷면이 나올 확률이 동일하지 않다고 가정하자. 이때 x=1일 확률은 매개변수 µ를 통해 다음과 같이 표현 가능하다. 여기에 다음 조건이 추가된다. 0

정보이론 정보 이론 정보 이론은 확률론 결정 이론 등과 함께 머신러닝 & 패턴인식에서 중요한 개념이다. 이번 글에서는 정보이론에 대해 소개한다. 이산확률 변수 x를 고려해보자. 이 변수가 특정 값을 가지고 있는 mldiary.tistory.com 위의 글에서 확률에서의 엔트로피의 개념에 대해 알아보았다. 이제 이 개념을 어떻게 패턴 인식에 활용할 수 있을 지 알아보자. 쿨백 라이블러 발산 알려지지 않은 분포 p(x)를 고려해보자. 이를 피팅하기 위해 모델을 만들었으며, (x)그 결과로 분포 q(x)를 구할 수 있었다고 하자. 만약 q(x)를 이용하여 x의 값을 수신자에게 전달하기 위해 코드를 만든다고 하면 p(x)가 아닌 q(x)를 사용했으므로 추가 정보가 필요하다. 이때 추가로 필요한 정보의 양은 다음..

정보 이론은 확률론 결정 이론 등과 함께 머신러닝 & 패턴인식에서 중요한 개념이다. 이번 글에서는 정보이론에 대해 소개한다. 이산확률 변수 x를 고려해보자. 이 변수가 특정 값을 가지고 있는 것을 확인했을 때 전달되는 정보의 양은 얼마만큼일까? 여기서 정보의 양은 '놀라움의 정도'로 생각할 수 있을 것이다. 매우 일어날 가능성이 높은 사건이 일어났다는 사실을 전해들었을 때보다 일어나기 매우 힘든 사건이 발생했다는 사실을 전해 들었을 때 더 많은 정보를 전달받는게 된다. 따라서 우리가 사용하게 될 정보량의 측정 단위는 해당 사건이 일어날 확률 p(x)의 종속적이게 된다. p(x)에 단조 함수인 정보량을 표현하는 함수 h(x)에 대해 살펴보도록 하자. 서로 연관되어 있지 않은(독립적인) 두 사건 x, y가 ..

오차 최소화 측면에서의 곡선 피팅 오차 최소화 측면에서의 곡선 피팅 곡선 피팅 N개의 관찰값 x로 이루어진 훈련 집합 x ≡ (x1,...,xN )T와 그에 해당하는 표적값 t ≡ (t1,...,tN )T가 주어졌다고 가정하자. 다음 그래프는 N=10 이고, sin(2πx) 함수에 가우시안 노이즈를 첨가 mldiary.tistory.com 확률적 측면에서의 곡선 피팅 확률적 측면에서의 곡선 피팅 앞선 글에서 다항식 곡선 피팅 문제를 오차 최소화의 측면에서 살펴보았다. 여기서는 같은 피팅 문제를 확률적 측면에서 살펴본다. 곡선 피팅 문제의 목표는 N개의 입력값 x = (x1, ... , xN)^T과 해 mldiary.tistory.com 앞서 소개한 다항식 곡선 피팅에서는 입력 변수가 오직 x 하나였다. ..

가우시안 분포는 단일 실수 변수 x에 대해 다음과 같이 정의된다(µ와 σ는 그래프의 개형을 결정짓는 변수이다). µ는 평균 σ^2은 분산, σ는 표준 편차에 해당한다. 또한 분산의 역수에 해당하는 값 β는 정밀도라고 한다(β = 1/σ^2) 위의 식으로부터 가우시안 분포가 두 조건을 만족한다는 것을 알 수 있다. 가우시안 분포를 따르는 x에 대한 함수의 기댓값은 다음과 같이 구할 수 있다. 연속 변수로 이루어진 D차원 벡터 x에 대한 가우시안 분포는 다음과 같다. D차원 벡터 µ는 평균값, D x D행렬 Σ는공분산이라 한다. |Σ|는 행렬식이다. 관측된 데이터 집합을 바탕으로 확률 분포의 매개변수를 결정하는 방법 중 하나는 가능도 함수를 최대화하는 매개 변수(µ, σ^2)를 찾는 것이다. 관측된 데이터 ..

많은 경우에 우리는 확률을 '반복 가능한 임의의 사건의 빈도수'라는 측면에서 바라본다. 이러한 해석을 빈도적 관점(frequentist)이라 일컫는다. 이에 맞서는 개념으로 이번장에서 다룰 베이지안(Bayesian)관점이 존재한다. 어떤 불확실한 사건에 대해 고려해 보자. 예를 들어, '공룡은 운석 충돌로 인해 멸종했다.'와 같은 사건을 생각해 보자. 이러한 사건들은 여러 번 반복할 수 없다. 따라서 앞서 살펴본 과일 상자 예시처럼 확률을 정의하는 것이 불가능하다. 그러나 우리는 이러한 사건들에 대해 견해 즉, 사전 지식을 가지고 있다. 예를 들어 '몇 억년 전 운석 충돌의 흔적이 발견 되었다.'와 같은 증거가 있다. 이러한 증거의 발견으로 인해 우리는 가지고 있던 사전 지식을 수정해 나갈 수 있다. 그..

확률 밀도 p(x)하에서 어떤 함수 f(x)의 평균값은 f(x)의 기댓값이라 하며 E[f]라 적는다. 이산 분포의 경우 기댓값은 다음과 같이 주어진다. 연속 변수의 경우에는 해당 확률 밀도에 대해 적분을 시행해서 기댓값을 구할 수 있다. 위의 기댓값에 대한 이해를 쉽게하기 위해 키를 예로 들어보자. 우리 나라 남성의 키를 확률 밀도 함수 p(x)로 나타내면, 170 중반을 중심으로 하는 정규 분포 형태의 그래프가 그려질 것이다. 만약 키의 평균 즉, 기대값을 구한다고 하면 위의 공식에서 f(x)는 단순히 x로 나타날 것이고 이를 계산하면 예측대로 E[f]는 170 중반의 값을 띄게 된다. 다변수 함수의 기댓값을 구할 경우에는 어떤 변수에 대해 평균을 내는지 지정하여 계산할 수 있다. 위의 식은 함수 f(..