ML Note

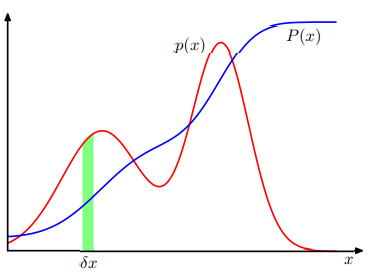
때때로 변수는 오렌지의 개수, 박스의 종류와 같이 셀수있는 것이 아니라 키, 몸무게와 같이 연속적인 경우가 있다. 이러한 경우 확률을 표현하는 데 있어 다른 방식을 사용해야 할 것이다. 이러한 연속적인 변수의 확률 p(x)를 확률 밀도(probability density)라고 부른다. 위의 그래프는 확률 밀도 함수의 예시이다. P(x)는 누적 분포 함수라고 부르며 p(x)의 적분값으로 볼 수 있다. p(x)는 확률 밀도 함수라고 부르며 P(x)의 미분값으로 볼 수 있다. 연속형 변수에서 어떤 특정한 값을 가질 확률을 구하는 것은 쉽지 않다. 예를 들어, 키가 임의의 한 사람의 키가 180일 확률을 구한다고 치자. 실제로 그의 키가 정확히 180일 확률 극히 희박하다. 따라서 우리는 179.5~180.5 ..

확률의 기본적인 컨셉을 이해하기 위해 다음 예시를 살펴보자 다음과 같이 빨간색, 파란색 상자 안에 사과(초록색)와 오렌지(주황색)이 들어있다고 가정하자. 여기서 랜덤하게 상자 하나를 골라 임의로 과일 하나를 꺼내고, 어떤 과일인지 확인 후 꺼냈던 상자에 다시 집어 넣는다고 하자. 이를 여러번 반복할 것이다. 이 과정에서 빨간 상자를 고를 확률이 40%, 파란 상자를 고를 확률이 60%이라고 가정하자. 여기서 상자는 바로 확률 변수이다. 상자를 확률 변수 B라고 하면 이 확률 변수 B는 r, b 두 개의 값을 가질 수 있다. 또한 과일의 정체 역시 확률 변수이며, 이를 F라고 지칭하자. 확률 변수 F는 a(사과), o(오렌지) 두 개의 값을 가질 수 있다. 빨간 상자를 고를 확률이 40%, 파란 상자를 고..

합의 법칙 다음 그림과 같은 상황을 고려해보자 행 방향이 확률 변수 X가 가질 수 있는 값 xi이고 열 방향이 확률 변수 Y가 가질 수 있는 값 yj이다. 여기서, X=xi이면서 Y=yj일 확률을 p(X=xi, Y=yj)로 적고 결합 확률이라고 칭한다. 이 결합 확률은 다음과 같이 표현된다. 여기서 nij는 xi이면서 yi일 경우의 수를 뜻하고 N은 전체 가능한 경우의 수를 뜻한다. 위의 그림을 통해서 다음과 같은 식 또한 도출할 수 있다. 위의 두 식을 이용하여 다음을 도출할 수 있다. 이것이 확률의 합의 법칙이다. 때때로 p(X=xi)는 주변 확률이라고 불린다. 곱의 법칙 X=xi인 사례들만 고려해보자. 그 중 Y=yj인 사례들의 비율을 생각해 볼 수 있다. 이를 조건부 확률이라고 하며 p(Y=yj ..