세 가지 결정 이론(오분류 비율 최소화, 기대 손실 최소화, 거부 옵션)
결정 이론(decision theory)란 불확실성이 존재하는 상황에서 최적의 의사결정을 내리는 방법에 대한 이론이다. 특히 분류 문제에서 여러가지 label값들 중 하나의 값의 확률이 100%로 나타나는 것이
mldiary.tistory.com
지금까지 분류 문제를 두 개의 단계로 나누어 보았다. 첫 번째는 추론 단계(inference stage)로 훈련 데이터셋을 활용하여 p(Ck|x)에 대한 모델을 학습시키는 단계이다. 두 번째는 결정 단계(decision stage)로 학습된 사후 확률들을 이용해서 최적의 클래스 할당을 시행하는 것이다. 두 가지 문제를 한 번에 풀어내는 방법을 생각해 볼 수도 있는데, x가 주어졌을 때 결정값을 돌려주는 함수를 직접 학습시키는 것이다. 이러한 함수를 판별 함수(discrimminant function)이라고 한다.
결정 문제를 푸는 데는 세 가지 다른 접근법이 있다. 이 세 가지 접근법은 모두 실제로 활용되고 있다.
1. 생성 모델
각각의 클래스 Ck에 대해 조건부 확률 밀도 p(x|Ck)를 알아낸다. 그 후 클래스별 사전 확률 p(Ck)도 구한다. 구한 값들을 베이지안 정리에 대입해 사후 확률을 간접적으로 알아낸다.
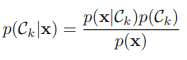
사후 확률을 구한 후에는 결정 이론을 적용하여 새 입력 변수 x에 대한 클래스를 구한다. 이러한 방식을 생성 모델(generative model)이라고 부른다. 왜냐하면 이렇게 만들어진 분포들로부터 표본을 추출함으로써 입력 공간에 합성 데이터 포인트들을 생성해 넣는 것이 가능하기 때문이다.
이러한 방식의 가장 큰 장점은 사후 확률을 구하는 과정에서 다른 방법론과는 달리 가능도에 해당하는 p(x|Ck)와 사전 확률 p(Ck)를 구할 수 있기 때문에 이를 이용하여 이상점 검출, 새 데이터 생성 등이 가능하다는 것이다. 그러나 이에 수반하는 단점으로 이상점 검출, 새 데이터 생성 등의 목적이 아닐 경우 불필요한 계산이 들어가 자원의 낭비가 일어난다는 것이다.

위의 그림을 통해 생성 모델의 특징을 알아보자. 생성 모델은 추론 과정에서 가능도에 해당하는 p(x|Ck)를 모델링하게 된다. 따라서 위의 그래프와 같은 모델이 만들어지는데, 사실 분류 문제에서는 위의 그림에서 붉은 그래프와 파란 그래프가 교차하는 지점 즉, 결정 경계를 찾아내는 것 만이 중요하다. 그 이외의 정보들은 필요가 없는데, 사실 이러한 결정 경계를 찾기 위해서 가능도 함수를 모델링한다는 것은 꽤나 큰 자원의 낭비이다. 다른 방법을 통해서 더욱 쉽게 결정 경계를 찾을 수도 있기 때문이다. 그러나 단순히 분류 문제에 국한하였을 때 가능도 함수가 낭비이지만, 앞서 언급한 것 처럼 이상점 검출, 새로운 데이터 생성 등의 목적이 있을 경우, 이러한 과정이 꼭 필요하게 된다.
2. 판별 모델
두 번째 방법은 사후 확률 p(Ck|x)를 구하되 생성 모델과 같이 베이즈 정리를 이용하여 사후 확률을 구하는 것이 아니라 사후 확률 자체를 직접 모델링하여 구하는 것이다. 그 후 결정 이론을 적용하여 입력 변수 x의 클래스를 구하는 이러한 방식을 판별 모델이라고 일컫는다. 분류 만이 목적일 경우 위의 생성 모델보다 자원의 낭비가 적어 효율적이다.
3. 판별 함수
각각의 입력값 x를 클래스에 할당하는 판별 함수 f(x)를 찾는다. 예를 들어, 두 개의 클래스를 가진 문제의 경우 f()는 이진값을 출력으로 가지는 함수로써, f=0일 경우 클래스 C1을, f=1일 경우 클래스 C2를 표현할 수 있다. 이 방식에서는 확률론이 사용되지 않는다.

이 방법의 목적은 위의 그래프에서 보이는 녹색 경계를 찾아내는 것이다. 이는 오분류의 확률을 최소화하는 결정 경계가 된다.
하지만 이 방법론의 경우 추론과 결정 단계에서 사후 확률 p(Ck|x)를 구하지 않는다는 것이다. 사후 확률을 구하지 않는다는 것은 생각보다 많은 문제를 불러일으키게 된다.
사후 확률을 알고 있을 때의 이점
위험의 최소화
손실 행렬의 값이 수시로 변하는 문제를 생각해보자. 만약 사후확률을 알고 있다면 손실 행렬을 수정함으로써 쉽게 최소 위험 결정 기준을 구할 수 있다 .반면 판별 함수만 알고 있을 경우 손실 행렬 값이 변할 때마다 데이터셋을 이용하여 분류 문제를 새로 풀어야 할 것이다.
거부 옵션
사후 확률을 알고 있으면 주어진 거부 데이터 포인트 비율에 대해 오분류 비율을 최소화하는 거부 기준을 쉽게 구할 수 있다.
클래스 사전 확률에 대한 보상
클래스의 데이터셋의 숫자에 균형이 맞지 않을 경우(암 환자 데이터보다 정상인 데이터가 훨씬 많을 것이다)이러한 데이터셋으로 학습한 모델은 일반화되기 어려울 수 있다. 왜냐하면 정상으로만 예측하여도 매우 높은 정확도를 나타낼 것이기 때문이다. 이러한 경우 부족한 데이터셋을 수정하여 비율을 올려주는 과정이 필요하다. 이런 기술을 적용한 경우 이후 클래스 사전 확률에 대한 보상을 추가해야 하는데 이 과정에서 사후 확률이 필요하다. 따라서 판별 함수를 사용하는 경우 이러한 기술을 적용할 수 없다.
모델들의 결합
복잡한 사례의 경우 하나의 큰 문제를 분리된 모듈로 해결하는 것이 바람직한 경우가 있다. 이런 경우 각각의 모듈이 사후확률을 제공한다면 단순히 모든 사후 확률을 합하는 것이 가능하다. 판별모델에서는 더욱 복잡한 과정이 요구된다.
'Machine Learning > Classification' 카테고리의 다른 글
| 세 가지 결정 이론(오분류 비율 최소화, 기대 손실 최소화, 거부 옵션) (0) | 2023.01.27 |
|---|---|
| 스태킹 앙상블 (Stacking Ensemble) (0) | 2022.08.05 |
| 부스팅(Boosting) - XGBoost, LightGBM (0) | 2022.08.04 |
| 배깅(Bagging) - 랜덤 포레스트(Random Forest) (2) | 2022.08.02 |
| Ensemble Learning - Voting(보팅) (1) | 2022.08.02 |