[논문] GMM-UBM (Gaussian Mixture Model - Universal Background Model)

이번 post는 "Speaker Verification Using Adapted Gaussian Mixture Models" D.Reynolds, et al, Digital signal processing (2000) 논문을 정리한다.

Pre-Deep learning의 화자 검증

 

위의 연대표는 SV(speaker verification)에서 시대별로 중요한 역할을 한 연구들이다. 이번 post에서는 GMM-UBM모델에 대해 다룬다. GMM-UBM은 1995년에 처음 소개된 방법으로 꽤 역사가 깊은 연구이다.

 

"Speaker Verification Using Adapted Gaussian Mixture Models" D.Reynolds, et al, Digital signal processing (2000)

Overview

---

GMM-UBM 모델의 전체 구조이다. Hypothesized speaker는 우리 모델이 이 화자의 목소리가 맞는지 아닌지 구분하는 정답이 된다. 이 Hypothesized speaker의 발화를 Fourier transform을 통해 MFCC로 추출한다. 그 후 이를 이용해 GMM(Gaussian mixture model)을 구성한다. 이렇게 생성된 목표 화자의 GMM을 다른 화자의 GMM과 비교(likelihood score)하여 화자 검증을 수행한다.

하지만 이렇게하면 hypothesized speaker의 샘플이 적을 경우, 모델의 분별력이 떨어질 수 있다. 화자의 GMM이 일반적인 발화의 GMM에서 너무 동떨어져 있어 해당 화자의 다른 발화를 들려주었을 때 목표 화자의 것이 아니라고 판단하는 문제가 쉽게 발생한다. 따라서 해당 논문에서는 UBM을 적용하여 문제를 해결한다. 어떻게 해결하는 지 논문을 따라가보자!

 

Log Likelihood ratio score

---

 

논문에서는 먼저 어떠한 기준으로 Decision을 내릴 것인지 소개하고 있다.

LLR score

 

위의 수식을 풀어서 보자. H0는 발화 Y가 hypothesized speaker S (타겟 화자)의 것이라는 가정이고, H1은 Y가 S의 것이 아니라는 가정이다. 즉 식은 간단하다.

(Y가 S의 것일 확률) / (Y가 S의 것이 아닐 확률) 

 

위의 식이 ɵ(threshold)보다 크면 H0을 채택하고, 작으면 H1을 채택하는 것이다(ɵ는 하이퍼 파라미터).

그림 아래의 LLR score식은 위의 식을 문자를 바꿔 decision 수식으로 정리한 것이다. 즉 p(X|λ)는

p(X|λ) -> 발화 X가 주인의 것일 확률

Decision을 어떻게 할 것인지는 정해졌다. 그럼 우리는 p(X|λ)를 계산하기만 하면 된다. 어떻게 계산해야 할까?

 

Gaussian Mixture Model (GMM)

---

논문에서는 p(X|λ)를 GMM 분포로 정의한다. 따라서 먼저 GMM을 이해해야 한다. 

SGM, GMM

 

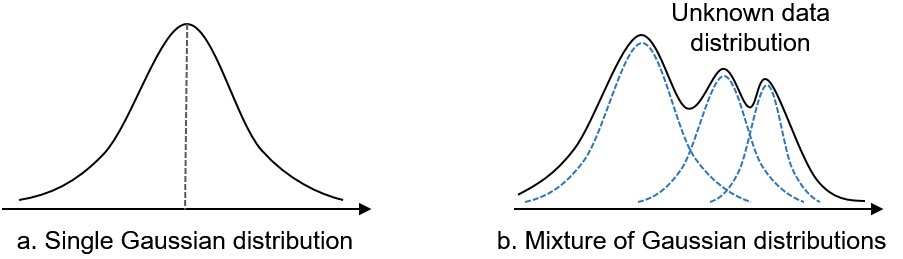
Single Gaussian model은 우리가 아는 정규 분포 모델이다. 하지만 single gaussian distribution은 파라미터가 μ(평균)과 σ(표준편차) 두 개 뿐이므로 표현할 수 있는 분포에 제한이 있다. 

Gaussian mixture model은 여러 개의 gaussian모델을 합쳐서 만든 모델이다. 오른쪽 그림을 보면 이해가 쉬울 것이다. 여러개의 gaussian model을 결합하여 모델의 표현력을 높인 것이다.

 

다시 우리 문제로 돌아가자. 우리는 p(X|λ)를 구해야 한다. 논문에서는 p(X| λ)를 다음과 같이 gaussian mixture로 정의한다.

p(X❘  λ)를 다음과 같이 gaussian mixture로 정의

 

M은 가우시안 mixture에 사용될 가우시안 분포의 개수이고, wi는 각 가우시안 분포의 가중치이다. pi(x)는 정확히 표현하면 pi(x|λ)이다. 위의 식에서 x가 벡터로 표현되어 있는 것을 알 수 있는데, 이는 x가 다차원을 가지고 있다는 것이다. 즉 위의 GMM그래프처럼 2차원 그래프를 상상하면 안된다. 그렇다면 x의 차원은 무엇일까?

x의 차원은 MFCC의 차원 수이다.

 

위의 정의를 천천히 생각해보자. 우리는 발화 x를 받았다. 이 발화는 오디오 파일로 주어질 것이다. 이 오디오 파일은 MFCC(80차원)로 변환된다. 그럼 이 MFCC features는 80차원 상의 한 점에 놓이게 될 것이다. 만약 이 feature가 여러 개 들어오게 된다면? 우리는 이를 분포로 표현할 수 있다. 즉 분포 p(X|λ)가 되는것이다. 80차원의 MFCC 샘플들로 만든 분포이기 때문에 p(X|λ)도 80차원이 된다. 이렇게 분포를 정의할 때 그냥 gaussian이 아닌 GMM을 쓰는 것 뿐이다. 표현력을 높이기 위해서.

 

p(X|λ)가 어떻게 GMM으로 정의되는지 정리가 되었다. 하지만 아직 문제가 남아있다. 화자의 발화 샘플로만 구성된 GMM은 너무 편향되어 있다. 따라서 타겟 화자의 다른 샘플이 들어와도 화자의 것이 아니라고 판단할 확률이 높아진다. 이를 논문에서는 UBM으로 해결하였다.

 

UBM (Universal Background Model)

---

Universal Background Model은 간단히 말해서 다양한 화자의 데이터를 이용해서 만든 GMM이다. 위의 타겟 화자를 포함한 모든 화자의 데이터를 GMM으로 만드는 것이다. 

즉, 타겟 화자 GMM의 편향 문제를 해결하기 위해 UBM에서 adaptation을 이용해 타겟 GMM을 만드는 방식을 사용한다.

 

MAP adaptation

 

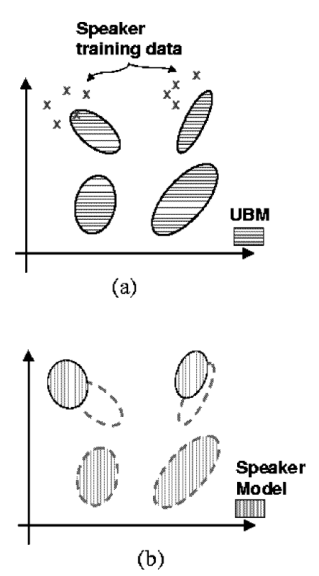
아무것도 없는 상태에서 타겟 화자의 데이터로만 GMM을 만드는 것보다 일반적인 background model에서 출발하는 것이 훨씬 generalization 측면에서 좋을 것이다. UBM에서 타겟 화자 발화 데이터를 이용해 새로운 GMM을 만드는 방식은 MAP Adptation을 채택했다.

MAP adaptation

 

수식은 MAP adaptation의 수학적 유도이다. 이 글에서는 따로 MAP의 수식적 원리는 설명하지 않고 넘어간다. 중요한 점은, GMM-UBM은 MAP adaptation 방법을 이용하여 target GMM의 generalization을 효과적으로 상승시켰다는 점이다.

 

Handset score normalization

---

GMM-UBM을 구현하면 Decision을 내릴 수 있다. 그러나 성능 향상을 위해 해주어야 하는 작업이 있다. 바로 Normalization이다.

논문이 출판된 시기(1990-2000년)를 감안하면 음성 데이터의 품질이 좋지 않았을 것이다. 특히 어떠한 채널을 통해 녹음을 했는지에 따라 음원 품질이 다르게 나타나는 현상이 있었다. 이러한 noise를 없애주기 위해 본 논문에서는 Handset score normalization을 적용했다.

Handset score normalization

 

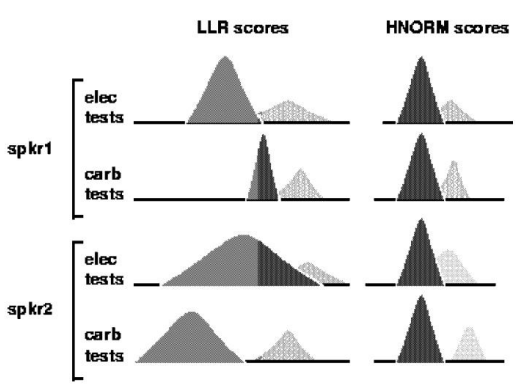
데이터셋은 ELEC(electret microphone handset)과 CARB(carbon-button microphone handset) 두 가지 환경에서 녹음되었다. 위의 그림을 보면 같은 화자가 다른 채널로 녹음했을 때 분포가 완전히 다르게 나타나는 것을 볼 수 있다. 이를 해결하기 위해 간단한 normalization 기법을 적용한다.

Normalization

 

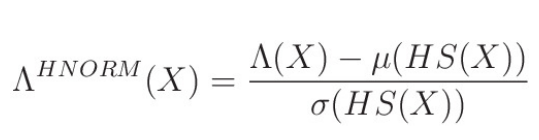
HS는 handset label이다. 즉, LLR score가 산출 되면, 여기서 해당 handset에 해당하는 모든 데이터의 평균 값을 빼주고, 표준편차로 나눠준다. 이러한 normalization 기법을 적용하면 위의 그림과 같이 같은 화자의 다른 채널에서 녹음한 데이터가 비슷한 경향을 나타내는 것을 확인할 수 있다.

 

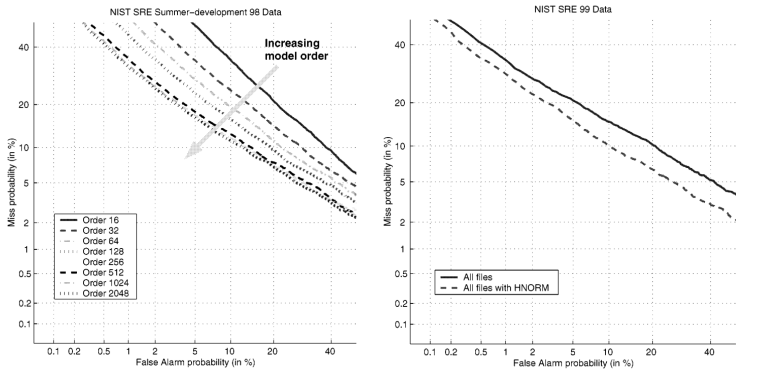
Experiments

---

Experiments