합/곱 알고리즘 (sum - product Algorithm) (tistory.com)
합/곱 알고리즘 (sum - product Algorithm)
인자 그래프 (tistory.com) 인자 그래프 그래프 모델의 추론 알고리즘을 알아보기 전에 이를 이해하는 데 필요한 새로운 형태의 그래프인 인자 그래프(factor graph)에 대해 알아보자. 인자 그래프는 각
mldiary.tistory.com
합/곱 알고리즘은 인자 그래프로 표현된 p(x)를 바탕으로 변수들에 대한 분포를 구할 수 있다. 그러나 우리는 종종 ¹가장 높은 확률을 가지는 변수들의 설정과, 그 ²해당 확률값을 알고싶을 때가 있다. 이를 구하기 위한 알고리즘이 최대 합 알고리즘이다.
이를 구하기 위해 가장 먼저 해볼 수 있는 생각이 합/곱 알고리즘을 이용하여 각각의 분포에 대해 해당 분포를 최대화하는 값을 찾는것이다. 이 경우 개별적으로 가장 확률이 높은 값을 찾을 수 있지만, 실전에서는 보통 결합적으로 가장 큰 확률을 가지는 값들을 찾는 것이 필요하다. 다시 말하자면 결합 분포를 최대화하는 벡터 xmax를 찾아햐 한다는 것이다. 다음 예시를 보자.
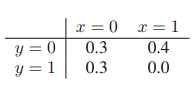
위의 그래프를 보면 x=0일 때 0.6, y=0일 때 0.7로 각각 높은 확률값을 가진다. 그러나 둘의 결합 분포는 0.3으로 x=1, y=0일 때보다 낮은 것을 볼 수 있다. 이처럼 개별 분포가 각각 최대의 확률값을 가지는 선택은, 결합 분포의 확률을 최대화 시키는 것이 아니라는 것을 알 수 있다.
최대 곱 알고리즘
결합 분포의 확률값을 최대화하는 최대 합 알고리즘을 구하기위해, 그 중간 과정인 최대 곱 알고리즘을 살펴보자. 우선, 우리는 xmax를 찾는 것이 목표이므로 max연산자를 사용하여 결합분포를 표현해보자.

p(x)는 예시로 자주 이용하였던 사슬 구조의 비방향성 그래프로 가정하자. 이 경우 포텐셜함수를 이용하여 다음과 같이 나타낼 수 있다.
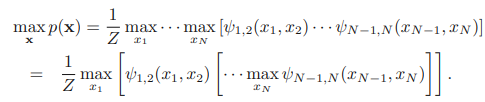
이때 max연산자와 곱연산자의 순서를 바꿔 위와 같이 나타낼 수 있다. 이러한 방법이 연산량을 줄일 수 있다는 것을 이전 글에서 알아보았다.
이제 식1을 다음 식을 통해 인자그래프로 변환한다.

그 후 위에서 예시로 든 것처럼 max연산자와 곱연산자의 순서를 바꾼다. 이 계산의 구조는 합/곱 알고리즘과 같으며 합/곱 알고리즘의 합 대신 max로 바뀐 것 뿐이다. 이제 특정 노드를 루트 노드로 정한 후 메시지를 잎에서 루트로 전달한다. 최종의 최대화 연산은 루트 노드에 도착한 모든 메시지들의 곱에 대해 시행되며, 이 결과가 p(x)들의 최댓값이다. 이 과정을 최대 곱 알고리즘(max-product)이라고 부른다.
최대 합 알고리즘 - 확률 최댓값 구하기
그런데 위의 최대 곱 알고리즘을 통해 작은 확률값들을 여럿 곱하면 수치적으로 언더플로우(underflow)문제가 발생한다. 따라서 결합 분포에 로그를 취해 곱을 합으로 바꾸는 것이 더 편리할 수 있다. 따라서 로그를 취해보도록 하자. 로그는 단조 함수이므로 최대 연산과 로그 함수는 교환할 수 있다.
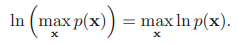
로그를 취했으므로 곱이 합으로 바뀌게 된다. 따라서 이를 최대 합 알고리즘(max-sum)이라고 일컫는다. 이 경우 잎 노드에서 최초로 보내지는 메시지는 다음과 같이 주어진다(합/곱 알고리즘 (sum - product Algorithm) (tistory.com) 여기에 결과에 루트가 취해진 것이다).

루트 노드에서의 확률값은 다음으로 주어진다.
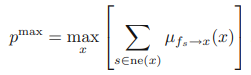
이는 합/곱 알고리즘의 p(x)값과 비슷하게 나타난다.
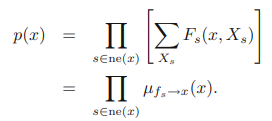
최대 합 알고리즘에서는 곱이 아니라 합으로 나타난 것과, max값이 취해진 것이 다른 점이다.
지금까지 최댓값을 구하는 방법에 대해 알아보았다. 그렇다면 글의 맨처음에 언급한 확률값은 구했으니 이번엔 변수의 설정을 구해보자.
최대 합 알고리즘 - 변수의 설정 구하기
지금까지 최대 확률값을 구하기 위해 루트 노드를 설정했고, 마지막 계산에서 루트 노드로 들어온 모든 메시지를 토대로 max값을 찾아냈다. 따라서 루트 노드에서 어떤 변수 설정이 최댓값인지 알고있다. 따라서 루트 노드의 변수 값으로로부터 시작해서 역으로 잎노드까지 가면서 하나씩 결합 확률을 최대를 만드는 변수설정을 찾아낼 수 있다. 변수들이 어떤 값일 때 각 변수들이 최대 상태를 가졌는지 계속 기록해 나가는 방식으로 이를 달성할 수 있다. 다시 말해, 다음의 값들을 저장하면 된다.
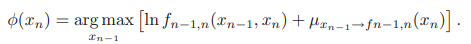
그런데 최대 확률값을 나타내는 변수의 설정이 하나가 아닐 수도 있다. 이와 같은 경우가 다음 그림에 나타나있다.
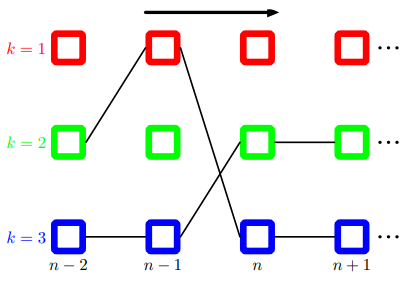
루트 노드 n에서 k=2일 때와 k=3일 때 모두 전역적 최댓값을 가진다고 하자. 이 경우 각각의 변수 설정에서 시작하여 역추적을 통해 변수 설정을 각각 구해낼 수 있다. 검은 화살표의 반대 방향으로 퍼져나가며 최대화시키는 변수 설정을 찾는 것이다.
'Machine Learning > Graph model' 카테고리의 다른 글
| 합/곱 알고리즘 (sum - product Algorithm) (0) | 2023.02.08 |
|---|---|
| 인자 그래프 (0) | 2023.02.08 |
| 그래프 모델에서의 추론 - 사슬 (0) | 2023.02.08 |
| 마르코프 무작위장 - 방향성 그래프와의 연관성 (0) | 2023.02.07 |
| 마르코프 무작위장 - 이미지 노이즈 제거 (0) | 2023.02.07 |