베이지안 네트워크를 이해하기 위해 베이지안 다항 회귀 예시를 생각해 보자. 여기서 확률 변수는 다항 계수의 벡터 w와 t = (t1, ... , tN)T 이다. t, w의 결합 분포는 확률의 곱의 법칙에 의해 다음과 같이 표현된다.

이 결합 분포를 다음과 같은 그래프 모델로 표현할 수 있다.

그래프의 노드가 '.......' 으로 연결된 것을 볼 수 있다. 이는 타깃 집합 벡터 t를 개개의 데이터 tn으로 표현하고자 할 때 노드를 생략하기 위해 위와 같이 표현한다. 그러나 위와 같이 표현하는 것도 간결하지 못하다. 따라서 이제는 대표 노드 tn을 그리고 판으로 둘러쌈으로써 표현할 것이다.

위의 결합 확률 모델은 많은 매개
변수들이 생략되어 있다. t, w로만 확률 분포를 표현하였는데 사실 이 결합 확률에는 많은 매개 변수들이 포함되어 있다. 이 경우 식을 다음과 같이 쓸 수 있다.

그래프 모델에서 확률 변수는 원으로, 결정적(deterministic) 매개변수들은 작은 점으로 표기하는 기존 관행에 따라 다음 그래프로 나타낼 수 있다.

머신 러닝 문제에서 관측값을 토대로 매개변수를 업데이트하기 때문에 특정 확률 변수는 관측값으로 설정해야 한다. 위의 그래프에서 관측값은 타겟 변수 tn이고 관측값은 음영을 추가하여 나타낸다.

w를 최적화 하는 문제에서는 베이즈 정리를 이용해 w에 대한 사후 분포로 나타내야 한다. w의 사후 분포는 다음과 같다.

그러나 대부분의 경우에서 w를 모델링 하는것 자체로는 그리 흥미롭지 않다. 우리의 최종 목표는 새로운 입력 변수 x^에 대해 t^를 예측하는 것이기 때문이다. 따라서 이를 포함한 확률 분포를 구한다고 가정하자. 이 모델의 모든 확률 변수에 대한 결합 분포는 다음과 같이 주어진다.
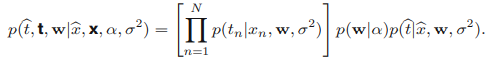
t^에 대한 예측 분포는 w에 대해 적분하여 없앰으로써 구할 수 있다.

이를 그래프 모델로 나타내면 다음과 같다.

'Machine Learning > Graph model' 카테고리의 다른 글
| 조건부 독립(conditional independence) (0) | 2023.02.05 |
|---|---|
| 선형 가우시안 모델 (0) | 2023.02.05 |
| 베이지안 네트워크 - 이산 변수 (0) | 2023.02.04 |
| 베이지안 네트워크 (0) | 2023.02.04 |
| 확률적 그래프 모델(probabilistic graphical model) (0) | 2023.02.04 |