곡선 피팅
N개의 관찰값 x로 이루어진 훈련 집합 x ≡ (x1,...,xN )T와 그에 해당하는 표적값 t ≡ (t1,...,tN )T가 주어졌다고 가정하자.

다음 그래프는 N=10 이고, sin(2πx) 함수에 가우시안 노이즈를 첨가하여 만든 타겟값들이다. 우리의 목표는 훈련 집합 x를 이용하여 새로운 입력값 x가 들어왔을 때 타겟 변수 t를 예측하는 것이다. 해당 곡선을 피팅하는 데 있어 다음과 같은 형태의 다항식을 활용한다.

다항함수 y(x,w)는 x에 대해서는 비선형이지만, 계수 w에 대해서는 선형이다. 우리는 위의 그래프에 파란 점에 해당하는 학습 데이터를 이용하여 새로운 x값이 들어왔을 때 t를 예측할 것이다. 따라서 위의 다항식을 이용하여 데이터가 어떤 형태로 분포하는지 표현하는 것이 목표이다. 그렇다면 어떻게 그래프를 피팅(fitting)할 수 있을까?
오차 함수(error function)
이는 오차 함수(error function)를 정의하고 이 함수의 값을 최소화하는 방법으로 피팅할 수 있다. 아래 함수는 가장 널리 쓰이는 오차 함수 중 하나이다.

여기서 xn은 n번째 데이터를 의미하고 w는 우리가 학습시킬 파라미터이다. tn은 n번째 데이터의 타겟값이다. 함수를 해석해보면, 우리가 예측한 값 y(xn,w)에서 실제 정답에 해당하는 tn과의 차를 구하고 이를 제곱하여 모든데이터에 대해 합산한 것이다. 여기서 제곱을 이용한 이유는 오차의 값을 항상 양수로 만들어 주기 위함이다. 이렇게 정의된 오차 함수는 우리가 예측한 값이 타깃값과 비슷하거나 일치할수록 더 낮은 값을 나타내게 된다. 아래 그래프는 MSE를 시각적으로 그래프로 표현한 것이다.

E(w)를 최소화하는 w를 선택함으로써 곡선 피팅 문제를 해결할 수 있다. 오차 함수가 2차 다항식의 형태를 지니고 있기 때문에 이 함수를 계수에 대해 미분(각각의 w들로 편미분)하면 w에 대해 선형인 식이 나온다. 따라서 이 오차 함수를 최소화하는 w는 유일한 값인 w*을 찾아낼 수 있고, 결과에 해당하는 다항식은 함수 y(x,w*)의 형태를 띠게 된다.
과적합(over fitting)
그런데 아직 다항식의 차수 M을 결정하는 문제가 남아있다. 이는 모델 비교 혹은 모델 결정이라 불리는 중요한 개념이다.다음 그림은 M = 0, 1, 3, 9 일 때의 그래프 피팅을 나타낸다.

파란 점이 학습 데이터이고, 초록색 선이 파란 점을 만드는 데 사용한 곡선이자 우리가 피팅해야 할 곡선이다. 빨간 선이 우리가 피팅한 곡선이다. M=0일 때, 그래프는 상수 함수를 띄게 되고 따라서 x축에 수평인 직선이 만들어진다. M=1일 때도 마찬가지로 거의 곡선을 피팅하지 못한다. M=9일 때는 빨간 곡선이 모든 파란 점(data point)를 지나가지만 초록색 선으로 피팅에는 실패했다. 이러한 경우를 과적합(over fitting)이라고 일컫는다. 과적합은 머신 러닝에서 항상 주의깊게 피해야 하는 요소로 고려된다. M=3일 경우 비로소 우리가 피팅하고자 하는 초록색 선에 근접한 것을 확인할 수 있었다.
이처럼 어떤 모델을 선택하느냐에 따라서 결과는 천차 만별이다. 어떤 모델은 심한 과적합을 일으킬 수 있고(M=9), 어떤 모델은 심한 일반화를 일으킬 수 있다(M=1).

다음 그래프를 통해 과적합의 문제를 알아보자. 파란색 그래프는 훈련 집합에 대한 오차함수이고, 빨간색 그래프는 sin(2πx)를 이용하여 새롭게 100개의 데이터를 생성한 후 피팅한 곡선을 이용하여 예측한 결과의 오차함수이다. 파란색 그래프를 보면 차수가 높아질수록 오차값이 낮아지는 것을 알 수 있다. 그러나 새로 생성한 데이터에 대한 예측 결과는 차수가 9일때 가장 안 좋은 성능을 보인다. 학습 데이터에 지나치게 과적합 되었기 때문이다.

또한 위의 표는 각각의 차수M를 가진 모델의 파라미터의 값을 보여주고 있는데, 모델의 차수가 커질수록 파라미터의 절대값이 매우 높아지는 것을 확인할 수 있다. 모든 학습 데이터 포인트를 지나게 하기 위해 그래프를 크게 변형시켰기 때문이다.

다음 그래프는 모델의 복잡도(M)은 그대로 두고 학습 데이터를 늘린 결과이다. 왼쪽의 15개 데이터를 이용한 그래프보다 오른쪽의 100개의 데이터를 이용한 그래프가 훨씬 더 초록색 선에 맞게 피팅된 것을 확인할 수 있다. 따라서 학습 데이터가 많을수록 정확히 피팅되고 과적합이 방지된다.
정규화항
많은 실제 사례에서 학습데이터의 수를 늘리는 것이 어려운 경우가 많다. 학습데이터 수를 늘리지 않고서 어떻게 과적합 문제를 해결할 수 있을까? 대표적인 기법이 바로 정규화(regularization)다.
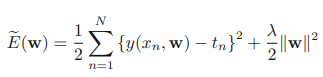
위의 오차 함수는 앞서 소개한 오차 함수 MSE에 정규화 항을 추가한 오차 함수이다. 정규화 항은 모든 계수들의 제곱합과 λ의 곱으로 이루어져 있다. λ는 정규화항의 중요도를 결정짓기 위한 초매개변수(hyper parameter)가 된다. 정규화항의 의미를 살펴보자. 앞서 소개한 표에서 과적합이 일어나면 w의 절대값이 증폭되는 것을 확인하였다. 따라서 만약 과적합이 일어나면 정규화항의 값 또한 증폭하게 되며, w의 개수인 M값이 커지게 되면 마찬가지로 정규화항의 값이 증폭할 것이다. 따라서 정규화항은 과적합이 될 수록 그 값이 커지게 되고 전체적으로 오차 함수의 값을 증가시키는 방법으로 과적합을 억제한다.
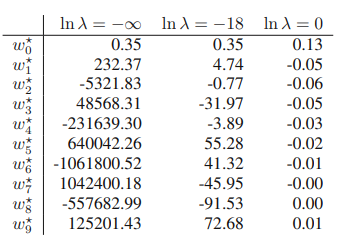
위의 표를 통해 정규화 항의 힘을 알 수 있다. λ가 0이면 정규화항을 삭제시키는 것이므로 ln λ = -∞ (λ=0)일 때 매개변수의 절대값이 매우 커지게 된다. 그러나 λ 값이 커짐에 따라 매개변수의 절대값이 점점 작아지는 것을 확인할 수 있다. 즉 과적합을 줄여나가는 것이다.
지금까지 살펴본 모델 피팅 기법을 바탕으로 모델 복잡도를 잘 선택하는 방법 하나를 생각해 볼 수 있다. 바로 데이터를 훈련 집합(training set)과 검증 집합(validation set)으로 나누는 것이다. 훈련 집합은 계수w를 결정하는 데 활용하고 검증 집합은 모델 복잡도(M이나 λ)를 최적화하는 데 활용하는 것이다. 이 방법은 보다 정밀하게 학습시킬 수는 있지만 소중한 데이터셋을 낭비하게 되므로 더 좋은 방법이 필요하다.
※이 글은 Christopher Bishop 교수님의 Pattern Recognition & Machine Learning을 공부하고 정리한 글입니다.
'Machine Learning > Regression' 카테고리의 다른 글
| 선형 회귀의 Gradient Descent (0) | 2023.02.01 |
|---|---|
| 선형 회귀 파라미터 최적화 - 최대 가능도 (0) | 2023.02.01 |
| 선형 회귀 - 선형 기저 함수 모델 (0) | 2023.02.01 |
| 회귀에서의 손실 함수 (0) | 2023.01.28 |
| 확률적 측면에서의 곡선 피팅 (0) | 2023.01.27 |