머신러닝 알고리즘의 성능을 가장 간단하게 올릴 수 있는 방법은 하이퍼 파라미터를 적절하게 튜닝하는 것이다. 이번 글에서는 대표적인 하이퍼 파라미터 튜닝 기법인 Grid Search와 베이지안 최적화에 대해 소개한다.
Hyper Parameter
하이퍼 파라미터란 학습 모델의 '설정'과도 같다. 모델 선언시 각각의 모델이 가진 설정을 변경하지 않는다면 기본값으로 설정되고, 모델은 이 설정을 참고하여 학습을 진행한다. 대표적인 하이퍼 파라미터로는 학습률(Learning Rate), 반복 횟수(Epoch, 주로 딥러닝에서 사용) 등이 있다.
각각의 학습 모델은 특정 하이퍼 파라미터 값의 조합에서 가장 높은 성능을 발휘한다. 이 조합은 같은 종류의 모델이더라도 데이터셋의 크기나 종류에 따라 완전히 다른 조합이 각 모델에서 최적의 성능을 나타낼 수 있다.
하이퍼 파라미터 튜닝을 통해서 큰 폭의 성능 향상을 기대하긴 어렵지만 대부분의 경우에서 튜닝 후 조금 더 좋은 성능을 나타내기 때문에 다른 기법들을 통해 성능을 최대한 끌어올린 후 마지막 수단으로 하이퍼 파라미터 튜닝을 진행하는 경우가 많다. 대표적인 하이퍼 파라미터 튜닝 기법으로는 Grid Search와 베이지안 최적화가 있다.
Grid Search
Grid는 격자라는 뜻으로 말그대로 격자처럼 촘촘하게 모든 조합을 수행한다는 의미이다. 기술한 하이퍼파라미터의 모든 조합을 한번 씩 수행하며 가장 높은 성능의 조합을 찾아낸다.
gird_search_param = {'max_depth': [1, 2, 3],
'min_samples_split': [3, 4] }
Grid Search로 튜닝할 하이퍼 파라미터를 다음과 같이 설정했다고 하자. max_depth는 1, 2, 3으로 변경해보고 min_sample_split을 3, 4로 변경해가며 최적의 조합을 찾는다. 따라서 총 성능 검사는 3 * 2 = 6번 진행하게 된다.
| max_depth | min_samples_split |
| 1 | 3 |
| 2 | 3 |
| 3 | 3 |
| 1 | 4 |
| 2 | 4 |
| 3 | 4 |
이렇게 각기 다른 6번의 조합 중 어떤 조합이 높은 성능을 나타내는 지 측정한다. 그렇다면 좋은 성능을 나타내는 것을 어떻게 확인할까? Grid Search는 교차검증(https://mldiary.tistory.com/3)을 기반으로 학습 후 테스트하여 Test Accuracy를 비교한다.
그렇다면 Grid Search는 총 몇 번의 학습을 진행할까? n 번재 하이퍼 파라미터의 옵션 개수를 Xn이라고 하고, 교차검증의 폴드 수를 cv라고 하면 다음과 같은 식이 성립한다.
X1 * X2 * X3 * . . . * Xn * cv
만약 3개의 하이퍼 파라미터를 각각 3개의 옵션으로 설정하여 3번의 교차검증을 한다고 하면 3 * 3 * 3 =27로 총 27번의 학습을 하게 된다. 데이터셋이 큰 경우 한 번의 학습도 시간이 적지 않게 소요되는 경우가 많은데 Grid Search를 이용하여 하이퍼 파라미터를 튜닝하려고 하면 너무 많은 시간이 소요될 수 있다. 혹은 튜닝하고싶은 하이퍼 파라미터가 너무 많은 경우 학습 횟수가 기하급수적으로 많아져 비효율적일 수 있다.
- 하나하나 꼼꼼하게 검사할 수 있다.
- 비교적 많은 시간이 소요된다.
- 적은 데이터셋, 검사할 하이퍼 파라미터가 적을 때 효율적으로 작동한다.
베이지안 최적화
Grid Search는 최적화 해야 할 하이퍼 파라미터 개수가 많을 경우 비효율적인 단점이 존재한다. 이를 극복하기 위해 제안된 최적화 기법이 베이지안 최적화이다.
Grid Search는 기본적으로 모든 가능한 조합을 하나씩 다 검사하지만 베이지안 최적화는 Random Search 즉, 이전에 검사한 하이퍼 파라미터 조합의 성능 결과를 기반으로 다음으로 검사할 하이퍼 파라미터 조합을 선정한다.
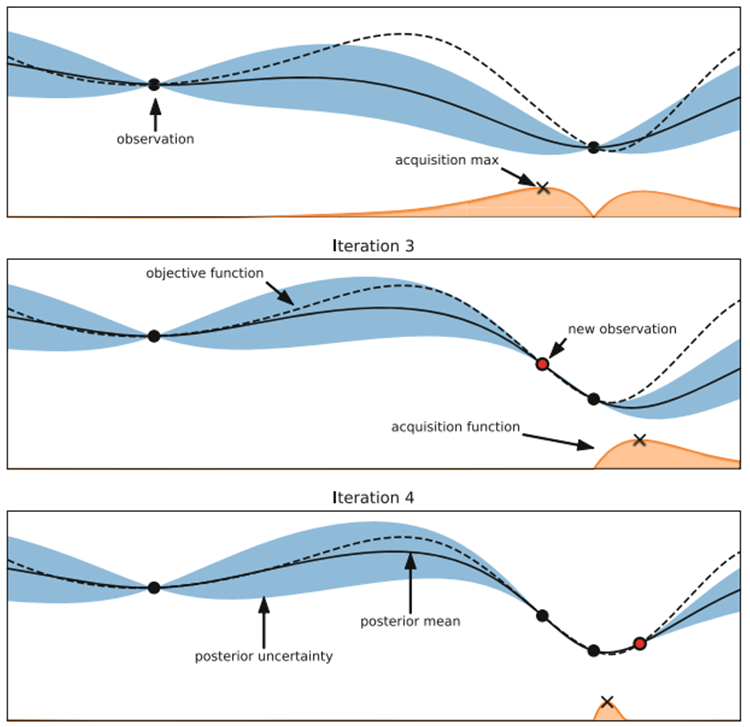
위의 그림은 베이지안 최적화를 그림으로 나타낸 것이다. x축은 하이퍼 파라미터 하나의 값이고 y축은 loss값이다(위의 그림에서는 최소 loss를 찾는 것이 목적이지만 우리의 목적은 최고 성능을 찾는 것이 목적이다). Test Accuracy를 나타낸다. 위의 그림과 같은 상황은 쉽게 그림으로 설명하기 위해 검사할 하이퍼 파라미터가 1개라고 가정한다. 따라서 2차원 평면에 그림으로 나타낼 수 있다. 실제로는 하이퍼 파라미터가 하나 늘어나면 늘어날수록 그래프의 차원도 하나 늘어나 여러개의 하이퍼 파라미터를 나타낼 경우 그림으로 그릴 수 없다.
첫 번째 그래프를 살펴보자 검은색 점은 하이퍼 파라미터를 이용하여 성능 검사를 측정한 결과이고, 점선은 objective function 즉, 우리가 맞춰야 할 그래프이다. 점선 그래프에서 가장 낮은 위치를 가리키는 하이퍼 파라미터가 최적의 하이퍼 파라미터이다. 실선은 현재 까지 검사한 검은 점들을 토대로 알고리즘이 예측한 가상의 objective function이고 파란색 영역은 예측한 실선의 신뢰 구간(오차 범위)이다. 알고리즘의 목적은 최고 성능을 가지는 검은 점을 찾는 것이기 때문에 오차 범위 그래프(하늘색)에서 최고값으로 나타나는 하이퍼 파라미터를 다음으로 검사한다(그림에서는 최저 loss를 찾기 때문에 오차 범위 그래프에서 최저값으로 나타나는 값을 다음으로 검사하고 있다). 이러한 과정을 여러 번 반복하면 오차범위 영역이 점차 좁아지며 예측 곡선(실선)이 objective function(점선)에 점차 가까워지게 되어 최적의 하이퍼 파라미터를 찾을 수 있다.
베이지안 최적화는 모든 조합을 순차적으로 다 검사하는 것이 아니라 확률적으로 최고의 성능을 나타낼 것이라고 예측되는 조합부터 우선적으로 검사하기 때문에 효율적으로 최적의 조합을 찾을 수 있으며, 이렇게 검사하는 횟수를 선언 시 지정해 줄 수 있기 때문에 튜닝해야 하는 하이퍼 파라미터가 많아도 걸리는 시간은 동일하다.
- 검사 횟수를 정해주기 때문에 하이퍼 파라미터가 많아도 걸리는 시간은 동일하다.
- 순차적으로 검사하지 않고 확률적으로 가장 유력한 하이퍼 파라미터를 먼저 검사하기 때문에 효율적이다.
- 튜닝해야 하는 하이퍼 파라미터가 많을수록 효율적이다.
'Machine Learning > Preprocessing' 카테고리의 다른 글
| SMOTE 오버샘플링 (0) | 2022.08.09 |
|---|---|
| 타이타닉 생존자 예측 (0) | 2022.05.09 |
| 피처 스케일링(feature scaling) (0) | 2022.05.08 |
| 데이터 인코딩 (Data Encoding) (0) | 2022.05.08 |
| 교차 검증 (Cross Validation) (0) | 2022.05.08 |